The complex number $1+\left(\sqrt{2}\right)\mathrm{i}$ is denoted by $u.$ The polynomial $x^4+x^2+2x+6$ is denoted by $\mathrm{p}\left(x\right).$ Check if $u$ is the root of $p\left(x\right)$. If yes, then find the other three roots of the equation $\mathrm{p}\left(x\right)=0.$

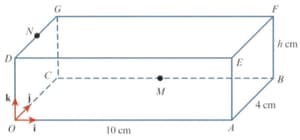
The diagram shows a cuboid $OABCDEFG$ with a horizontal base $OABC$. The cuboid has a length $OA$ of $10 \mathrm{cm},$ a width $AB$ of $4 \mathrm{cm}$ and a height $BF$ of $h \mathrm{cm}.$ The point $M$ is the midpoint of $CB$ and the point $N$ is the point on $DG$ such that $\overrightarrow{ON}=\mathrm{j}+3\mathrm{k}.$ The unit vectors $\mathrm{i}, \mathrm{j}$ and $\mathrm{k}$ are parallel to $OA, OC$ and $OD,$ respectively.

Write down the value of $h.$

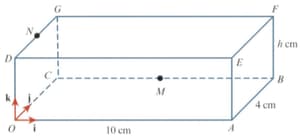
The diagram shows a cuboid $OABCDEFG$ with a horizontal base $OABC$. The cuboid has a length $OA$ of $10 \mathrm{cm},$ a width $AB$ of $4 \mathrm{cm}$ and a height $BF$ of $h \mathrm{cm}.$ The point $M$ is the midpoint of $CB$ and the point $N$ is the point on $DG$ such that $\overrightarrow{ON}=\mathrm{j}+3\mathrm{k}.$ The unit vectors $\mathrm{i}, \mathrm{j}$ and $\mathrm{k}$ are parallel to $OA, OC$ and $OD,$ respectively.

Find the unit vector in the direction $\overrightarrow{ON}.$

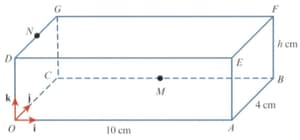
The diagram shows a cuboid $OABCDEFG$ with a horizontal base $OABC$. The cuboid has a length $OA$ of $10 \mathrm{cm},$ a width $AB$ of $4 \mathrm{cm}$ and a height $BF$ of $h \mathrm{cm}.$ The point $M$ is the midpoint of $CB$ and the point $N$ is the point on $DG$ such that $\overrightarrow{ON}=\mathrm{j}+3\mathrm{k}.$ The unit vectors $\mathrm{i}, \mathrm{j}$ and $\mathrm{k}$ are parallel to $OA, OC$ and $OD,$ respectively.

Find angle $NME.$

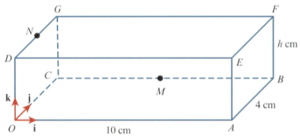
The diagram shows a cuboid $OABCDEFG$ with a horizontal base $OABC$. The cuboid has a length $OA$ of $10 \mathrm{cm},$ a width $AB$ of $4 \mathrm{cm}$ and a height $BF$ of $h \mathrm{cm}.$ The point $M$ is the midpoint of $CB$ and the point $N$ is the point on $DG$ such that $\overrightarrow{ON}=\mathrm{j}+3\mathrm{k}.$ The unit vectors $\mathrm{i}, \mathrm{j}$ and $\mathrm{k}$ are parallel to $OA, OC$ and $OD,$ respectively.

Find, in the form $r=a+\lambda b,$ a vector equation of the line $MF.$

The variables $x$ and $y$ are related by the differential equation $\frac{\mathrm{d}y}{ \mathrm{d}x}=\frac{6x{\mathrm{e}}^{3x}}{y^2}.$

It is given that $y=2$ when $x=0.$ Solve the differential equation and hence find the value of $y$ when $x=0.5,$ giving your answer correct to $2$ decimal places.

On an Argand diagram, sketch the loci of points representing complex numbers $w$ and $z$ such that $|w-1-2\mathrm{i}|=1$ and $\arg (z-1)=\frac{3}{4}\pi .$

Calculate the least value of $\left|w-z\right|$ for points on these loci.