The diagram shows a cuboid $OABCDEFG$ with a horizontal base $OABC.$ The cuboid has a length $OA$ of $8 \mathrm{cm},$ a width $AB$ of $4 \mathrm{cm}$ and a height $BF$ of $d \mathrm{cm}.$ The point $M$ is the midpoint of $CE$ and the point $N$ is the point on $GF$ such that$GN=6 \mathrm{cm}.$ The unit vectors $i, j$ and $k$ are parallel to $OA, OC$ and $OD,$ respectively. It is given that $\overrightarrow{OM}=4i+2j+k.$

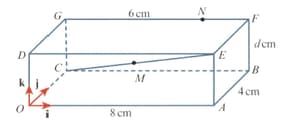
Find $\overrightarrow{ON}.$

The diagram shows a cuboid $OABCDEFG$ with a horizontal base $OABC.$ The cuboid has a length $OA$ of $8 \mathrm{cm},$ a width $AB$ of $4 \mathrm{cm}$ and a height $BF$ of $d \mathrm{cm}.$ The point $M$ is the midpoint of $CE$ and the point $N$ is the point on $GF$ such that$GN=6 \mathrm{cm}.$ The unit vectors $i, j$ and $k$ are parallel to $OA, OC$ and $OD,$ respectively. It is given that $\overrightarrow{OM}=4i+2j+k.$

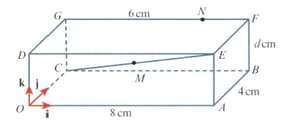
Find the unit vector in the direction $\overrightarrow{MN}.$

The position vectors of the points $A, B, C$ and $D$ are given by $a, b, c$ and $d,$ respectively, where

$a=\left(\begin{array}{l}2\\ 2\\ 0\end{array}\right),b=\left(\begin{array}{c}13\\ 5\\ 4\end{array}\right),c=\left(\begin{array}{r}5\\ -3\\ 4\end{array}\right)$ and $d=\left(\begin{array}{r}-6\\ -6\\ 0\end{array}\right).$

Find $\left|\overrightarrow{AD}\right|, \left|\overrightarrow{BC}\right|, \left|\overrightarrow{AB}\right|$ and $\left|\overrightarrow{DC}\right|.$

The position vectors of the points $A, B, C$ and $D$ are given by $a, b, c$ and $d,$ respectively, where

$a=\left(\begin{array}{l}2\\ 2\\ 0\end{array}\right),b=\left(\begin{array}{c}13\\ 5\\ 4\end{array}\right),c=\left(\begin{array}{r}5\\ -3\\ 4\end{array}\right)$ and $d=\left(\begin{array}{r}-6\\ -6\\ 0\end{array}\right).$

Deduce that $ABCD$ is a parallelogram.

The position vectors of the points $A, B, C$ and $D$ are given by $a, b, c$ and $d,$ respectively, where

$a=\left(\begin{array}{l}2\\ 2\\ 0\end{array}\right),b=\left(\begin{array}{c}13\\ 5\\ 4\end{array}\right),c=\left(\begin{array}{r}5\\ -3\\ 4\end{array}\right)$ and $d=\left(\begin{array}{r}-6\\ -6\\ 0\end{array}\right).$

Find the coordinates of the point $M,$ the midpoint of the line $AB$

The position vectors of the points $A, B, C$ and $D$ are given by $a, b, c$ and $d,$ respectively, where

$a=\left(\begin{array}{l}2\\ 2\\ 0\end{array}\right),b=\left(\begin{array}{c}13\\ 5\\ 4\end{array}\right),c=\left(\begin{array}{r}5\\ -3\\ 4\end{array}\right)$ and $d=\left(\begin{array}{r}-6\\ -6\\ 0\end{array}\right).$

Find the coordinates of the point $P$ such that $\left|\overrightarrow{BP}\right|=\frac{1}{3}\left|\overrightarrow{BD}\right|.$

Relative to an origin$O,$ the position vector of $A$ is $i-2j+5k$ and the position vector of $B$ is $3i+4j+k.$

Find the magnitude of $\overrightarrow{AB}.$

Relative to an origin$O,$ the position vector of $A$ is $i-2j+5k$ and the position vector of $B$ is $3i+4j+k.$

Use Pythagoras' theorem to show that $OAB$ is a right-angled triangle.

Relative to an origin$O,$ the position vector of $A$ is $i-2j+5k$ and the position vector of $B$ is $3i+4j+k.$ Find the exact area of triangle $OAB.$