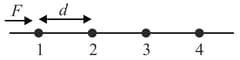
The diagram shows a string of equally placed beads of mass $m$, separated by distance $d$. The beads are free to slide without friction on a thin wire. A constant force $F$ acts on the first bead initially at rest till it makes collision with the second bead. The second bead then collides with the third and so on. Suppose that all collisions are elastic.

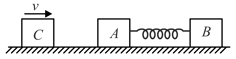
Two blocks $A$ and $B$ each of mass $\mathrm{m}$, are connected by a massless spring of natural length $L$ and spring constant $k$. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in diagram. A third identical block $C$, also of mass $\mathrm{m}$, moves on the floor with a speed $v$ along the line joining $A$ and $B$, and collides elastically with $A$. Then:- 

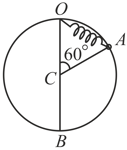
A particle of mass $5 \mathrm{kg}$ is free to slide on a smooth ring of radius $r=20 \mathrm{cm}$ fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed the top point $O$ of the ring. Initially the particle is at rest at a point $A$ of the ring such that $\angle OCA=60°$, $C$ being the centre of the ring. The natural length of the spring is also equal to $r=20 \mathrm{cm}$. After the particle is released and slides down the ring the contact force between the particle & the ring becomes zero when it reaches the lowest position $B$. Determine the force constant of the spring.

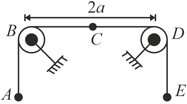
A light string $ABCDE$ whose mid point is $C$ passes through smooth rings $B$ and $D$, which are fixed in a horizontal plane distance $2a$ apart. To each of the points $A,C$ and $E$ is attached a mass $m$. Initially $C$ is held at rest at $O$ (mid point $BD$) and is then set free. What is the distance $OC$ in meter when $C$ comes to instantaneous rest?

(Given $a=3\mathrm{m}$)

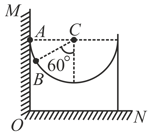
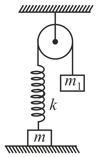
For what minimum value of $m_1$ in $\mathrm{kg}$ for which the block of mass $m$ will just leave the contact with surface? (Given: $m=8\mathrm{kg}$)

A ball of mass $1 \mathrm{kg}$ is released from position, A inside a fixed wedge with a hemispherical cut of radius $0.5 \mathrm{m}$ as shown in the figure. If the force exerted by the vertical wall $OM$ on wedge, when the ball is in position $B$, is $F$ then find the value of $\frac{F}{\sqrt{3}}$ in $N$. (neglect friction everywhere) (Take $g=10 {\mathrm{ms}}^{-2}$)