The diagram shows a triangular prism, $OABCDE.$ The uniform cross-section of the prism, $OAE,$ is a right-angled triangle with base $24 \mathrm{cm}$ and height $7 \mathrm{cm}.$ The length, $AB,$ of the prism is $20 \mathrm{cm}.$ The unit vectors $i, j$ and $k$ are parallel to $\overrightarrow{OA},\overrightarrow{ OC}$ and $\overrightarrow{OE,}$ respectively. The point $N$ divides the length of the line $DB$ in the ratio $2 : 3.$

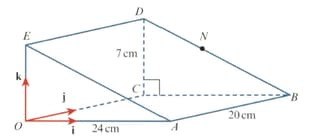
Find $\overrightarrow{ON}.$

Three points $O, P$ and $Q$ are such that $\overrightarrow{OP}=2\hat{i}+5\hat{j}+a\hat{k}$ and $\overrightarrow{OQ}=\hat{i}+\left(1+a\right)\hat{j}-3\hat{k}$. Given that the magnitude of $\overrightarrow{OP}$ is equal to the magnitude of $\overrightarrow{OQ},$ find the value of the constant $a.$

Relative to an origin $O,$ the position vectors of the points $P$ and$Q$ are given by $\overrightarrow{OP}=\left(\begin{array}{c}-6k\\ -2\\ 8(1+k)\end{array}\right)$ and $\overrightarrow{OQ}=\left(\begin{array}{c}2k+13\\ -8\\ -32k\end{array}\right).$

Given that $OPQ$ is a straight line find the value of the constant $k$.

Relative to an origin $O,$ the position vectors of the points $P$ and$Q$ are given by $\overrightarrow{OP}=\left(\begin{array}{c}-6k\\ -2\\ 8(1+k)\end{array}\right)$ and $\overrightarrow{OQ}=\left(\begin{array}{c}2k+13\\ -8\\ -32k\end{array}\right).$

Given that $OPQ$ is a straight line:

write each of $\overrightarrow{OP}$ and $\overrightarrow{OQ}$ in the form $xi+yj+zk$

Relative to an origin $O,$ the position vectors of the points $P$ and$Q$ are given by $\overrightarrow{OP}=\left(\begin{array}{c}-6k\\ -2\\ 8(1+k)\end{array}\right)$ and $\overrightarrow{OQ}=\left(\begin{array}{c}2k+13\\ -8\\ -32k\end{array}\right).$

Given that $OPQ$ is a straight line:

If the magnitude of the vector $\overrightarrow{PQ}$ is $3\sqrt{n}$, then the value of $n$ is

An ant has an in-built vector navigation system! It is able to go on complex journeys to find food and then return directly home (to its starting point) by the shortest route.
An ant leaves home and its journey is represented by the following list of displacements:

$i+3j+6k \left(\begin{array}{l}1\\ 6\\ 0\end{array}\right) 10i \left(\begin{array}{c}-3\\ -1\\ -5\end{array}\right) 4i-k$

The ant finds food at this point.

What single displacement takes the ant home?

One unit of displacement is $10 \mathrm{cm}.$

What is the shortest distance home from the point where the ant finds food?

Do quadratic expressions of the form $a{x}^2+bx+c$, where $a, b$ and $c$ are real constants, form a vector space? Explain your answer.

Show that the scalar product has the following properties:

$a·b=b·a$

$a·mb=ma·b= m(a·b)$, where $m$ is a scalar

$a·(b + c)= a·b+a·c$

$(a + b)·(c+d)=a·c+a·d+b·e+b·d$

Find which of the following pairs of position vectors are perpendicular to one another.

For any position vectors that are not perpendicular, find the acute angle between them.

$a=\left(\begin{array}{r}2\\ 8\\ -2\end{array}\right), b=\left(\begin{array}{r}7\\ -1\\ 3\end{array}\right)$