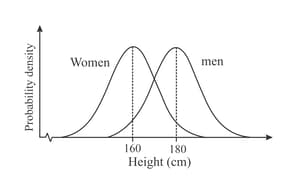
The distributions of the heights of $1000$ women and of $1000$ men both produce normal curves, as shown. The mean height of the women is $160 \mathrm{cm}$ and the mean height of the men is $180 \mathrm{cm}.$ The heights of these women and men are now combined to form a new set of data. Assuming that the combined heights also produce a normal curve, copy the graph opposite and sketch onto it the curve for the combined heights of the $2000$ women and men.

Probability distributions for the quantity of apple juice in $500$ apple juice tins and for the quantity of peach juice in $500$ peach juice tins are both represented by normal curves.
The mean quantity of apple juice is $340 \mathrm{ml}$ with variance $4 {\mathrm{ml}}^2$ and the mean quantity of peach juice is $340 \mathrm{ml}$ with standard deviation 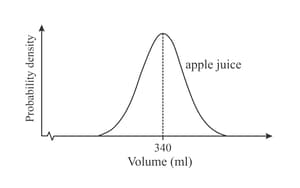$4 \mathrm{ml}.$

Copy the diagram and sketch onto it the normal curve for the quantity of peach juice in the peach juice tins.

Probability distributions for the quantity of apple juice in $500$ apple juice tins and for the quantity of peach juice in $500$ peach juice tins are both represented by normal curves.
The mean quantity of apple juice is $340 \mathrm{ml}$ with variance $4 {\mathrm{ml}}^2,$ and the mean quantity of peach juice is $340 \mathrm{ml}$ with standard deviation 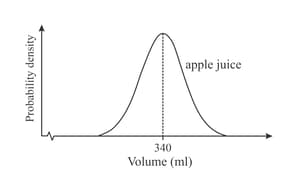$4 \mathrm{ml}.$

Describe the curves' differences and similarities.

The values in two datasets, whose probability distributions are both normal curves, are summarised by the following totals:
$\Sigma x^2=35000, \Sigma x=12000$ and $n=5000.$
$\Sigma y^2=72000, \Sigma y=26000$ and $n=10000.$

Show that the centre of the curve for $y$ is located to the right of the centre of the curve for $x.$

The values in two datasets, whose probability distributions are both normal curves, are summarised by the following totals:
$\Sigma x^2=35000, \Sigma x=12000$ and $n=5000.$
$\Sigma y^2=72000, \Sigma y=26000$ and $n=10000.$

On the same diagram, sketch a normal curve for each dataset.

Given that $Z~\mathrm{N}(0,1),$ find the following probability correct to $3$ significant figures.

$P (Z<0.567)$

Given that $Z~\mathrm{N}(0,1),$ find the following probability correct to $3$ significant figures.

$P (Z\le 2.468)$