The electric field inside a sphere which carries a charge density proportional to the distance from the origin $\rho =\alpha r$ ($\alpha$ is a constant) is:

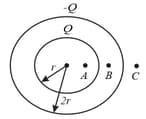
Consider two thin uniformly charged concentric shells of radii $r$ and $2r$ having charges $Q$ and $-Q$ respectively, as shown. Three points $A, B$ and $C$ are marked at distances $\frac{r}{2}, \frac{3r}{2}$ and $\frac{5r}{2}$ respectively from their common centre. If $E_A, E_B$ and $E_C$ are magnitudes of the electric fields at points $A, B$ and $C$ respectively, then, 

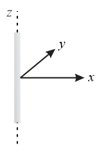
An infinitely long wire is kept along $z$-axis from $z=-\infty$ to $z=+\infty$, having uniform linear charge density $\frac{10}{9} \mathrm{nC} {\mathrm{m}}^{-1}$. The electric field at the point $(6 \mathrm{cm}, 8 \mathrm{cm}, 10 \mathrm{cm})$ will be, 

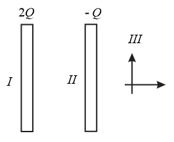
Two large conducting thin plates are placed parallel to each other. They carry the charges as shown. The variation of magnitude of electric field in space due to this system is best given by, 

A positively charged sphere of radius $r_0$ carries a volume charge density $\rho$ (see figure). A spherical cavity of radius $\frac{r_0}{2}$ is then scooped out and left empty, as shown. $C_1$ is the centre of the sphere and $C_2$ is the centre of the cavity. What is the direction and magnitude of the electric field at point $B$?

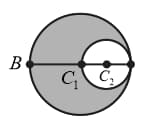
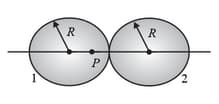
The figure shows, in cross-section, two solid spheres with uniformly distributed charge throughout their volumes. Each has a radius $R$. The point lies on a line connecting the centres of the spheres, at a radial distance $\frac{R}{2}$ from the centre of the sphere $1$. If the net electric field at a point $P$ is zero, what is the ratio $\frac{q_2}{q_1}$ of the total charges?