The equation of a wave travelling on a string is, $y=(0.10 \mathrm{mm})\sin \left[\left(31.4 {\mathrm{m}}^{-1}\right)x+\left(314 {\mathrm{s}}^{-1}\right)t\right]$.

(a) The wave speed, the wavelength and the frequency of the wave are $\alpha \mathrm{m} {\mathrm{s}}^{-1}, \beta \mathrm{cm} \text{and} \gamma \mathrm{Hz}$ respectively.

(b) The maximum displacement and the maximum speed of a portion of the string are $\delta \mathrm{mm} \text{and} \eta \mathrm{cm} {\mathrm{s}}^{-1}$ respectively.

Then, the value of $\left(\alpha +\beta +\gamma +\delta +\eta \right)$ is:

A wave travels along the positive $x-$direction with a speed of $20 \mathrm{m} {\mathrm{s}}^{-1}$. The amplitude of the wave is $0.20 \mathrm{cm}$ and the wavelength is $2.0 \mathrm{cm}$.

(a) Wave equation which describes this wave is given by $y=(0.20 \mathrm{cm})\sin \left[\left(\pi {\mathrm{cm}}^{-1}\right)x-\left(2\pi \times {10}^{\alpha } {\mathrm{s}}^{-1}\right)t\right]$

(b) The displacement and velocity of the particle at $x=2.0 \mathrm{cm}$ at time $t=0$ according to the wave equation is given as $\beta cm$ and $\gamma \pi cm s^{-1}$.

Find the value of $\alpha \beta \gamma$.

A wave is described by the equation, $y=(1.0 \mathrm{mm})\mathrm{sin\pi }\left(\frac{x}{2.0 \mathrm{cm}}-\frac{t}{0.01 \mathrm{s}}\right)$.

(a) The time period and the wavelength is given as $\beta ms$ and $\alpha cm$ respectively.

(b) The speeds of the particles at $x=3.0 \mathrm{cm}$, $5.0 \mathrm{cm}$ and $7.0 \mathrm{cm}$ at $t=0.01 \mathrm{s}$ is given as $\gamma mm s^{-1}$.

Find the value of $\alpha \beta \gamma .$

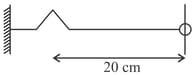
The figure below shows a plot of the transverse displacements of the particles of a string at $t=0$ through which a travelling wave is passing in the positive x-direction. The wave speed is $20 \mathrm{cm} {\mathrm{s}}^{-1}$. Find the frequency$\left(\mathrm{Hz}\right)$ of the wave.

A wave travelling on a string at a speed of $10 \mathrm{m} {\mathrm{s}}^{-1}$ causes each particle of the string to oscillate with a time period of $20 \mathrm{ms}$.

(a) What is the wavelength of the wave?

(b) If the displacement of a particle is $1.5 \mathrm{mm}$ at a certain instant, what will be the displacement of a particle $10 \mathrm{cm}$ away from it at the same instant?

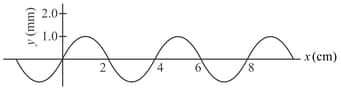
A string of length $20 \mathrm{cm}$ and linear mass density $0.40 \mathrm{g} {\mathrm{cm}}^{-1}$ is fixed at both ends and is kept under a tension of $16 \mathrm{N}$. A wave pulse is produced at $t=0$ near an end as shown in the figure, which travels towards the other end.
(a) When will the string have the shape shown in the figure again.(b) Sketch the shape of the string at a time half of that found in part (a).

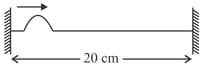
A string of linear mass density $0.5 \mathrm{g} {\mathrm{cm}}^{-1}$ and a total length $30 \mathrm{cm}$ is tied to a wall at one end and to a frictionless ring at the other end (as shown in the figure). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of $20 \mathrm{cm} {\mathrm{s}}^{-1}$. The pulse is symmetric about its maximum which is located at a distance of $20 \mathrm{cm}$ from the end joined to the ring.

$\left(a\right)$ Assuming that the wave is reflected from the ends without loss of energy, The time taken by the string to regain its shape is given as $\alpha s$. $\left(b\right)$ The shape of the string changes periodically with time, its time period is given as $\beta s.$ $\left(c\right)$ The tension in the string is given as $\gamma \times {10}^{-3} N$.

Find the value of $\alpha \beta \gamma$.