The fastest possible rate of rotation of a planet is that for which the gravitational force on material at the equator barely provides the centripetal force needed for the rotation. (Why?) 

(i) Show then that the corresponding shortest period of rotation is given by $\mathrm{T}=\sqrt{\frac{3\pi }{\mathrm{Gp}}}$ where $\rho$ is the density of the planet, assumed to be homogeneous.

(ii) Evaluate the rotation period assuming a density of $3.0\mathrm{gm} {\mathrm{cm}}^{-3}$ typical of many planets, satellites, and asteroids. No such object is found to be spinning with a period shorter than found by this analysis.

In a particular double star system, two stars of mass $3.22\times {10}^{30} \mathrm{kg}$ each revolve about their common centre of mass, $1.12\times {10}^{11} \mathrm{m}$ away.

(i) Calculate their common period of revolution, in years.

(ii) Suppose that a meteoroid (small solid particle in space) passes through this centre of mass moving at right angles to the orbital plane of the stars. What must its speed be if it is to escape from the gravitational field of the double star?

Consider two satellites $A$ and $B$ of equal mass $m$, moving in the same circular orbit of radius $r$ around the Earth $E$ but in opposite sense of rotation and therefore on a collision course (see figure).

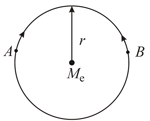
In terms of $G,M_e,m$ and $r$ the total mechanical energy $E_A+E_B$ of the two satellite plus Earth system before collision is given by$\frac{-\beta G{\mathrm{mM}}_e}{r}$ then find the value of $\beta$ .

Consider two satellites $A$ and $B$ of equal mass $m$, moving in the same circular orbit of radius $r$ around the Earth $E$ but in opposite sense of rotation and therefore on a collision course (see figure).

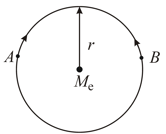
If the collision is completely inelastic so that wreckage remains as one piece of tangled material (mass $=\mathit{2}m$), the total mechanical energy immediately after collision is given by $-\frac{a{\mathrm{GmM}}_e}{\mathrm{r}}$. Find $a$.

Consider two satellites $A$ and $B$ of equal mass $m$, moving in the same circular orbit of radius $r$ around the Earth $E$ but in opposite sense of rotation and therefore on a collision course (see figure).

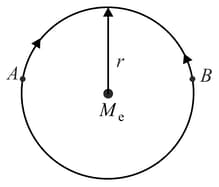
Describe the subsequent motion of the wreckage.