The figure given below is a section of a conducting rod of radius $R_1=1.30 \mathrm{mm}$ and length $L=11.00 \mathrm{m}$ inside a thin-walled coaxial conducting cylindrical shell of radius$R_2=10.0 R_1$ and the (same) length $L.$ The net charge on the rod is $Q_1=-5.22\times {10}^{-13} \mathrm{C};$ that on the shell is $Q_2=-2.00 Q_1$. What are the (a) magnitude $E$ and (b) direction (radially inwards or outwards) of the electric field at radial distance $r=2.00 R_2?$ What are (c) $E$ and (d) the direction at $r=5.00 R_1?$ What is the charge on the (e) interior and (f) exterior surface of the shell?

In figure $\left(a\right)$,

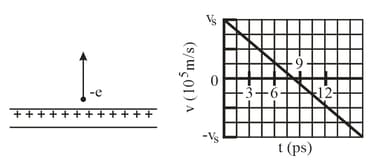
An electron is shot directly away from a uniformly charged plastic sheet, at speed, $v_{\mathrm{s}}=1.6\times {10}^5 \mathrm{m} {\mathrm{s}}^{-1}$. The sheet is nonconducting, flat, and very large.

In figure $\left(b\right)$,

The electron's vertical velocity component, $\left(v\right)$ versus time $\left(t\right)$, until the return to the launch point is given.

What is the charge density of the sheet's surface?

$\left(a\right) \left(b\right)$

An unknown charge sits on a conducting solid sphere of radius $10 \mathrm{cm}$. If the electric field $30 \mathrm{cm}$ from the center of the sphere has the magnitude $3.0\times {10}^{3 }\mathrm{N} {\mathrm{C}}^{-1}$ and is directed radially inwards, then 

$\left(A\right)$ what is the net charge on the sphere?

$\left(B\right)$ what is the charge density?

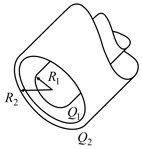
A charge of uniform linear density $1.5 \mathrm{nC} {\mathrm{m}}^{-1}$ is distributed along a long, thin, nonconducting rod. The rod is coaxial with a long conducting cylindrical shell (inner radius$=5.0 \mathrm{cm}$ and outer radius$=10 \mathrm{cm}$). The net charge on the shell is zero.

$\left(A\right)$ What is the magnitude of the electric field $15 \mathrm{cm}$ from the axis of the shell?

What is the surface charge density on the

$\left(B\right)$ inner surface of the shell?

$\left(C\right)$ outer surface of the shell?

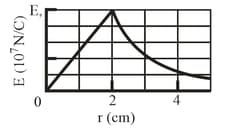
The figure gives the magnitude of the electric field inside and outside a sphere with a positive charge distributed uniformly throughout its volume. The scale of the vertical axis is set by $E_s=10\times {10}^7 \mathrm{N} {\mathrm{C}}^{-1}$. $\left(a\right)$ What is the charge on the sphere? $\left(b\right)$ What is the field magnitude at $r=8.0 \mathrm{m}?$

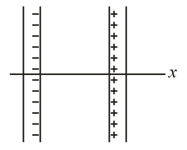
ln the figure, two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have excess surface charge densities of opposite signs and magnitude $2.31\times {10}^{-22} \mathrm{C} {\mathrm{m}}^{-2}.$ In unit vector notation, what is the electric field at points,$\left(a\right)$ to the left of the plates,
$\left(b\right)$ to the right of them and $\left(c\right)$ between them?

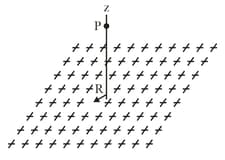
In figure a small circular hole of radius $R=1.30 \mathrm{cm}$ has been cut in the middle of an infinite, flat, nonconducting surface that has uniform charge density$\text{σ}=4.50 \mathrm{pC} {\mathrm{m}}^{-2}$. A $z$-axis, with its origin at the hole's center, is perpendicular to the surface. In unit vector notation, what is the electric field at point $P$ at $z=2.56 \mathrm{cm}$?