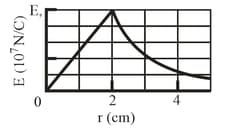
The figure gives the magnitude of the electric field inside and outside a sphere with a positive charge distributed uniformly throughout its volume. The scale of the vertical axis is set by $E_s=10\times {10}^7 \mathrm{N} {\mathrm{C}}^{-1}$. $\left(a\right)$ What is the charge on the sphere? $\left(b\right)$ What is the field magnitude at $r=8.0 \mathrm{m}?$

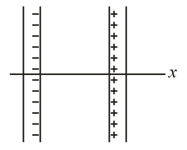
ln the figure, two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have excess surface charge densities of opposite signs and magnitude $2.31\times {10}^{-22} \mathrm{C} {\mathrm{m}}^{-2}.$ In unit vector notation, what is the electric field at points,$\left(a\right)$ to the left of the plates,
$\left(b\right)$ to the right of them and $\left(c\right)$ between them?

In figure a small circular hole of radius $R=1.30 \mathrm{cm}$ has been cut in the middle of an infinite, flat, nonconducting surface that has uniform charge density$\text{σ}=4.50 \mathrm{pC} {\mathrm{m}}^{-2}$. A $z$-axis, with its origin at the hole's center, is perpendicular to the surface. In unit vector notation, what is the electric field at point $P$ at $z=2.56 \mathrm{cm}$?

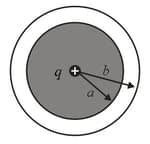
In figure, a nonconducting spherical shell of inner radius $a=1.50 \mathrm{cm}$ and outer radius $b=2.40 \mathrm{cm}$ has (within its thickness) a positive volume charge density $\text{ρ}=A/r$ where $A$ is constant and $r$ is the distance from the center of the shell. In addition, a small ball of charge $75.0 \mathrm{fC}$ is located at that center. What value should $\mathrm{A}$ have if the electric field in the shell $(a\le r\le b)$ is to be uniform?

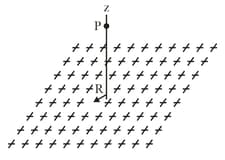
The figure shows a very large nonconducting sheet that has a uniform surface charge density of $\sigma =-2.00 \mu \mathrm{C} {\mathrm{m}}^{-2}$; it also shows a particle of charge $Q=8.00 \mu \mathrm{C},$ at distance $d$ from the sheet. Both are fixed in place. If $d=0.200 \mathrm{m},$ at what $\left(a\right)$ positive and $\left(b\right)$ negative coordinate on the $x$ axis (other than infinity) is the net electric field ${\overrightarrow{E}}_{\text{net }}$ of the sheet and particle zero? $\left(c\right)$ If $d=0.950 \mathrm{m},$ at what coordinate on the $x$ axis is ${\overrightarrow{E}}_{\text{net }}=0?$

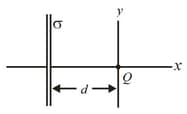
Figure shows a section of a long, thin-walled metal tube of radius $R=2.50 \mathrm{cm},$ with a charge per unit length of $\lambda =2.00\times {10}^{-8} \mathrm{C} {\mathrm{m}}^{-1}$. What is the magnitude $E$ of the electric field at radial distance (a) $r=\frac{R}{2.00}$ and (b) $r=2.00 R?$ (c) Graph $E$ versus $r$ for the range $r=0$ to $2.00 R$.

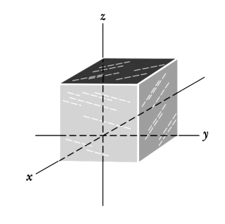
The cube in figure has edge length $1.40 \mathrm{m}$ and is oriented as shown in a region of uniform electric field. Find the electric flux through the right face if the electric field, in newtons per coulomb, is given by (a) $19.0\hat{\mathrm{i}},$ (b)$-2.00\hat{\mathrm{j}},$  and (c) $-20.0\hat{\mathrm{i}}+4.00\hat{\mathrm{k}}$  (d) What is the total flux through the cube for each field? (e) What is the total flux if the edge length is doubled?

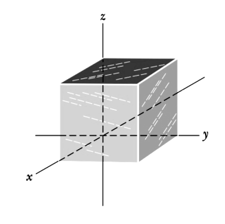
At each point on the surface of the cube shown in the figure, the electric field is parallel to the $z$ axis. The length of each edge of the cube is $4.0 \mathrm{m}$. On the top face of the cube the field of $\overrightarrow{E}=-34 \hat{\mathrm{k}}\mathrm{N} {\mathrm{C}}^{-1}$ and on the bottom face it is $\overrightarrow{E}=+20 \hat{\mathrm{k}}\mathrm{N} {\mathrm{C}}^{-1}$ . Determine the net charge contained within the cube.