EASY
12th ICSE
IMPORTANT
Earn 100
The kinetic energy of a proton is equal to the energy of a photon. If be the (de-Broglie) wavelength of the proton and that of the proton, then the ratio is proportional to:
(a)
(b)
(c)
(d)
50% studentsanswered this correctly

Important Questions on Matter Waves
EASY
12th ICSE
IMPORTANT
MEDIUM
12th ICSE
IMPORTANT
MEDIUM
12th ICSE
IMPORTANT
EASY
12th ICSE
IMPORTANT
HARD
12th ICSE
IMPORTANT
Light of wavelength falls on a cathode plate inside a vacuum tube as shown in the figure. The work function of the cathode surface is and the anode is a wire mesh of conducting material kept at a distance from the cathode. A potential difference is maintained between the electrodes. If the minimum de-Broglie wavelength of the electrons passing through the anode is , which of the following statement is true?
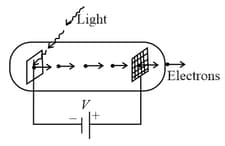
HARD
12th ICSE
IMPORTANT
MEDIUM
12th ICSE
IMPORTANT
HARD
12th ICSE
IMPORTANT
