The period $\mathrm{T}$ of a simple pendulum is related to its length $l$ by the equation:

$\mathrm{T}=2\pi \sqrt{\frac{l}{g}}$

 A graph is plotted with ${\mathrm{T}}^2$ on the $y$ -axis and $l$ on the $x$ -axis. Express the gradient in terms of $g$.

The time period $\mathrm{T}$ of a simple pendulum is related to its length $l$ by the equation:

$\mathrm{T}=2\pi \sqrt{\frac{l}{g}}$

Where $g$ is the acceleration of free fall.

A student measures the time $t$ for $10$ oscillations for different lengths $l$. This table shows her data.

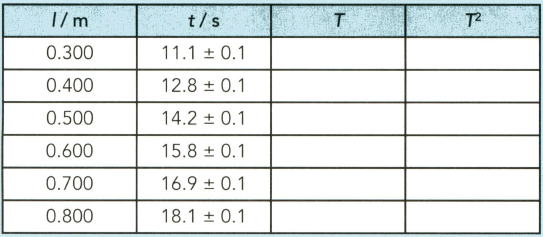
(i) Calculate and record values of $\mathrm{T} \& {\mathrm{T}}^2$, including the absolute uncertainties in $\mathrm{T} \& {\mathrm{T}}^2$.

The time period $T$ of a simple pendulum is related to its length $l$ by the equation:

$T=2\pi \sqrt{\frac{l}{g}}$

Where $g$ is the acceleration of free fall.

 A student measures the time $t$ for $10$ oscillations for different lengths $l$. This table shows her data.

 Plot a graph of $T^2\left(se{c}^2\right)$ against $l\left(m\right)$ including error bars for $T^2$ .

The time period $T$ of a simple pendulum is related to its length $l$ by the equation:

$T=2\pi \sqrt{\frac{l}{g}}$

Where $g$ is the acceleration of free fall.

A student measures the time $t$ for $10$ oscillations for different lengths $l$. This table shows her data.

Draw a straight line of best fit and a worst acceptable line on your graph.

The period $T$ of a simple pendulum is related to its length $L$ by the equation:

$T=2\pi \sqrt{\frac{L}{g}}$

Where $g$ is the acceleration of free fall.

A student measures the time $t$ for $10$ oscillations for different lengths $L$. This table shows her data.

Determine the gradient of your line and include the uncertainty in your answer.

The period $T$ of a simple pendulum is related to its length $l$ by the equation:

$T=2\pi \sqrt{\frac{l}{g}}$

Where $g$ is the acceleration of free fall.

A student measures the time $t$ for $10$ oscillations for different lengths $l$. This table shows her data.

Use your value of the gradient to determine $g$ and include the absolute uncertainty in your value.

The period $T$ of a simple pendulum is related to its length $l$ by the equation:

$T=2\pi \sqrt{\frac{l}{g}}$

Where $g$ is the acceleration of free fall.

A student measures the time $t$ for $10$ oscillations for different lengths $l$. This table shows her data.

Using the value of $g$ and its uncertainty, calculate the value of $t$ when the length $l$ is $0.900 \mathrm{m}$. Include the absolute uncertainty in your answer.

Readings are taken of the resistance $R$ of a thermistor at different temperatures $T$. It is suggested that the relationship between $R$ and $T$ is $R=k{T}^n$, where $k$ and $n$ are constants. A graph is plotted with $\log \left(R\right)$ on the y-axis and $\log \left(T\right)$ on the x-axis. State the value of the gradient and the y-intercept in terms of $k$ and $n$.

Readings are taken of the resistance $R$ of a thermistor at different temperatures $T$. It is suggested that the relationship between $R$ and $T$ is $R=k{T}^n$, where $k$ and $n$ are constants. Values for $T$ and $R$ are shown in the given table:

Complete the table and include absolute uncertainties in $\log \left(\mathrm{R}/\mathrm{\Omega }\right)$.