A bucket in the form of a frustum of a cone of height 30 cm with radii of its lower and upper ends as 10 cm and 20 cm , respectively. Find the capacity of the bucket. Also find the cost of milk which can completely fill the bucket at the rate of ₹ 40 per litre. Use π = 22 7

Given that, a bucket in the form of a frustum of a cone of height 30 cm with radii of its lower and upper ends as 10 cm and 20 cm , respectively. Capacity of the bucket can be obtained by finding the volume of the frustum of cone. We know that, volume of the frustum of cone = 1 3 πh r 1 2 + r 2 2 + r 1 r 2 Where, h is the height the frustum of the cone, r 1 , r 2 are the radii of both ends of the frustum. Using the formula mentioned above, Capacity = 1 3 × 22 7 × 30 20 2 + 10 2 + 20 × 10 = 22 7 × 10 400 + 100 + 200 = 22 7 × 10 × 700 = 22 × 10 × 100 = 22000 cm 3 = 22 litre [ ∵ 1 litre = 1000 cm 3 ] Cost of 22 litre milk = Cost of 1 litre milk × 22 = ₹ 40 × 22 = ₹ 880 Hence, the capacity of the bucket is 22 litre and the cost of milk is ₹ 880 .

MEDIUM

10th CBSE

IMPORTANT

Earn 100

The radii of the circular ends of a bucket of height $15 c m$ and $14 c m$ and $r c m (r < 14) .$ If the volume of the bucket is $5390 c m^{3},$ then find the value of $r .$

Important Questions on Surface Areas and Volumes

MEDIUM

10th CBSE

IMPORTANT

CBSE Syllabus Standard Mathematics for Class X>Chapter 14 - Surface Areas and Volumes>Exercise 14.4>Q 7

A cone is of height $24 c m$ and the base radius $9 c m .$ Find the radius of the circular section cut from the cone by a plane parallel to the base and $8 c m$ from it.

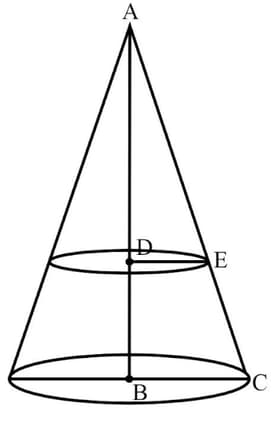
Question Image

MEDIUM

10th CBSE

IMPORTANT

CBSE Syllabus Standard Mathematics for Class X>Chapter 14 - Surface Areas and Volumes>Exercise 14.4>Q 8

The perimeters of the ends of a frustum of a (solid) cone are

36 c m

and

48 c m

. If the height of the frustum is

11 c m,

, find its volume.

MEDIUM

10th CBSE

IMPORTANT

CBSE Syllabus Standard Mathematics for Class X>Chapter 14 - Surface Areas and Volumes>Exercise 14.4>Q 9

The diameter of the lower and upper ends of a bucket (in the form of a frustum of a cone) are

10 c m

and

30 c m

Respectively . If its height is

24 c m

, find the capacity of the bucket.

MEDIUM

10th CBSE

IMPORTANT

CBSE Syllabus Standard Mathematics for Class X>Chapter 14 - Surface Areas and Volumes>Exercise 14.4>Q 9

The diameter of the lower and upper ends of a bucket in the form of a frustum of a cone are

10 cm

and

30 cm

respectively. If its height is

24 cm,

find the area of the metal sheet used to make the bucket. [Use

π = 3.14]

HARD

10th CBSE

IMPORTANT

CBSE Syllabus Standard Mathematics for Class X>Chapter 14 - Surface Areas and Volumes>Exercise 14.4>Q 10

The radii of the ends of a frustum of a cone

45 c m

45 cm high are

28 c m

28 cm and

7 c m .

7 cm Find its volume, curved surface area and the total surface area.

MEDIUM

10th CBSE

IMPORTANT

CBSE Syllabus Standard Mathematics for Class X>Chapter 14 - Surface Areas and Volumes>Exercise 14.4>Q 11

A tent consists of a frustum of a cone, surmounted by a cone. If the diameters of the upper and lower circular ends of the frustum be

14 m

and

26 m

respectively, the height of the frustum be

8 m

and the slant height of the surmounted conical portion be

12 m

, find the area of the canvas required to make the tent in square metres. (Assume that the radii of the upper circular ends of the frustum and the base of the surmounted conical portion are equal. Use

π = \frac{22}{7}

)

MEDIUM

10th CBSE

IMPORTANT

CBSE Syllabus Standard Mathematics for Class X>Chapter 14 - Surface Areas and Volumes>Exercise 14.4>Q 12

A container open at the top, is in the form of a frustum of a cone of height 24cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container at the rate of

₹ 21

per litre.

MEDIUM

10th CBSE

IMPORTANT

CBSE Syllabus Standard Mathematics for Class X>Chapter 14 - Surface Areas and Volumes>Exercise 14.4>Q 13

A container open at the top and made up of metal sheet is in the form of a frustum of a cone of height 16cm with diameters of its lower and upper ends as

16 c m

and

40 c m

respectively . Find the cost of metal sheet to make the container , if it costs

₹ 10

per

100 c m^{2}

(

Use

π = 3.14)

The radii of the circular ends of a bucket of height 15 cm and 14 cm and r cm (r<14). If the volume of the bucket is 5390cm3, then find the value of r.

Important Questions on Surface Areas and Volumes

Learn and Prepare for any exam you want !

The radii of the circular ends of a bucket of height $15 c m$ and $14 c m$ and $r c m (r < 14) .$ If the volume of the bucket is $5390 c m^{3},$ then find the value of $r .$