The velocity of liquid $(v)$ in steady flow at a location through cylindrical pipe is given by $v=v_{0}\left(1-\frac{r^{2}}{R^{2}}\right)$, where $r$ is the radial distance of that location from the axis of the pipe and $R$ is the inner radius of pipe, if $R=10 \mathrm{~cm}$, volume rate of flow through the pipe is $\pi / 2 \times 10^{-2} \mathrm{~m}^{3} \mathrm{~s}^{-1}$ and the coefficient of viscosity of the liquid is $0.75 \mathrm{~N} \mathrm{~s} \mathrm{~m}^{-2}$

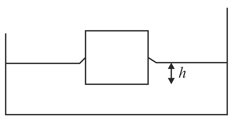
A cube of side $a$ and mass $m$ just floats on the surface of water as shown in the figure. The surface tension and density of water are $T$ and ${\rho }_w$, respectively. If angle of contact between cube and water surface is zero, find the distance $h$ (in metres) between the lower face of cube and surface of the water.
(Take $m=1 \mathrm{kg}, g=10 \mathrm{m}{ \mathrm{s}}^{-2}, aT=\frac{10}{4}$ unit and ${\rho }_w{a}^{2}g=10$ unit )

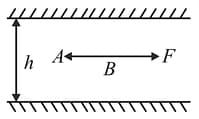
A thin plate $AB$ of large area $A$ is placed symmetrically in a small gap of height $h$ filled with water of viscosity ${\eta }_0$ and the plate has a constant velocity $v$ by applying a force $F$ as shown in the figure. If the gap is filled with some other liquid of viscosity $0.75 {\eta }_0$, at what minimum distance (in $cm$ ) from minimum distance (in $\mathrm{cm}$ ) from top wall should the plate be placed in the gap, so that the plate can again be pulled at the same constant velocity $V$, by applying the same force $F ?$ (Take $h=20 \mathrm{cm}$ )