This is a stress- strain graph for a metal wire.

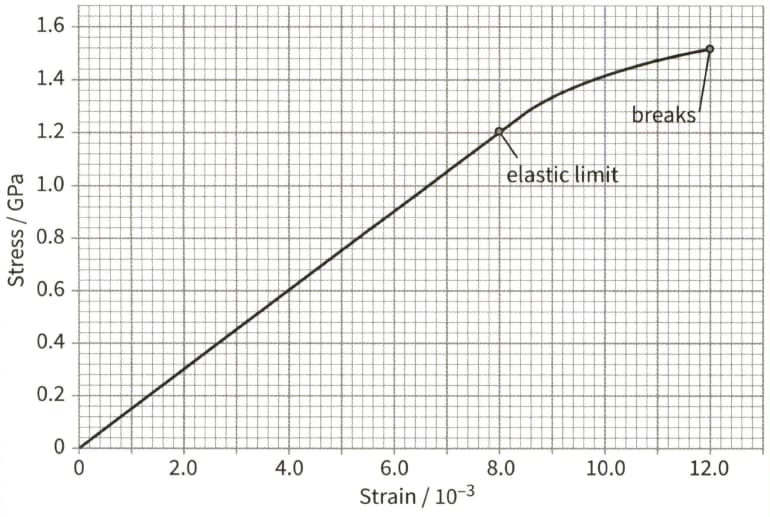
The wire has a diameter of $0.84\mathrm{mm}$ and a natural length of $3.5\mathrm{m}$. Use the graph to determine:

(a) The Young modulus of the wire

This is a stress- strain graph for a metal wire.

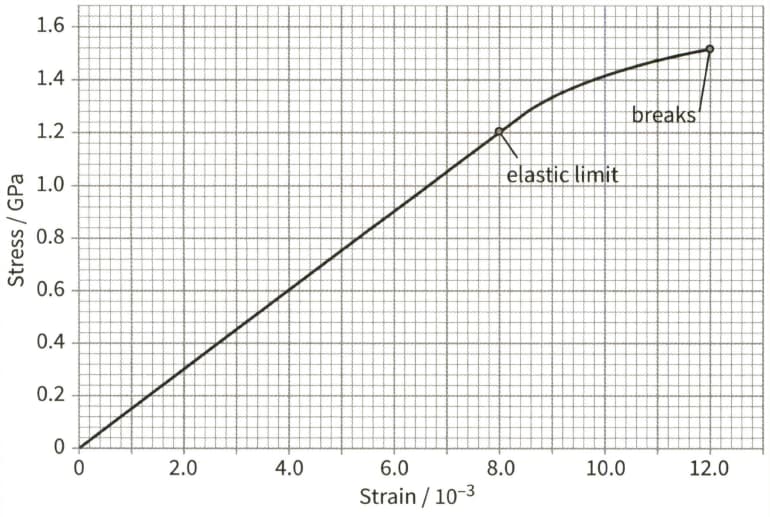
The wire has a diameter of $0.84\mathrm{mm}$ and a natural length of $3.5\mathrm{m}$. Use the graph to determine:

(b) The extension of the wire when the stress is 0.60GPa

This is a stress- strain graph for a metal wire.

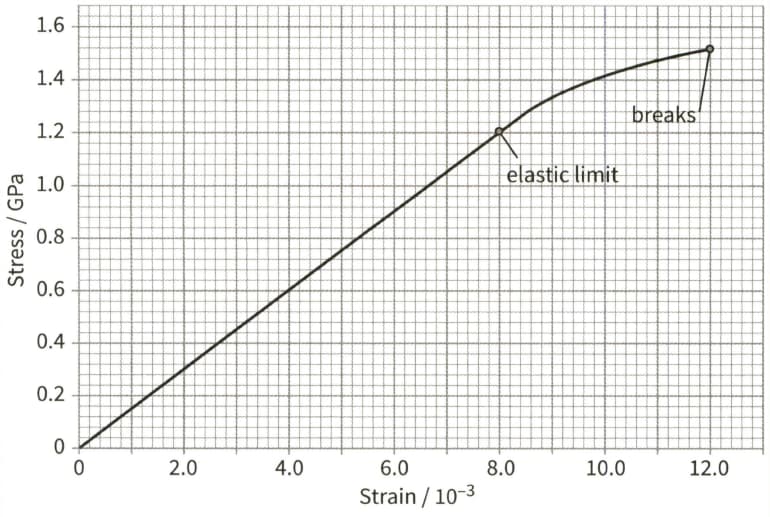
The wire has a diameter of $0.84\mathrm{mm}$ and a natural length of $3.5\mathrm{m}$. Use the graph to determine:

(c) the force that causes the wire to break, assuming that the cross-sectional area of the wire remains constant

This is a stress- strain graph for a metal wire.

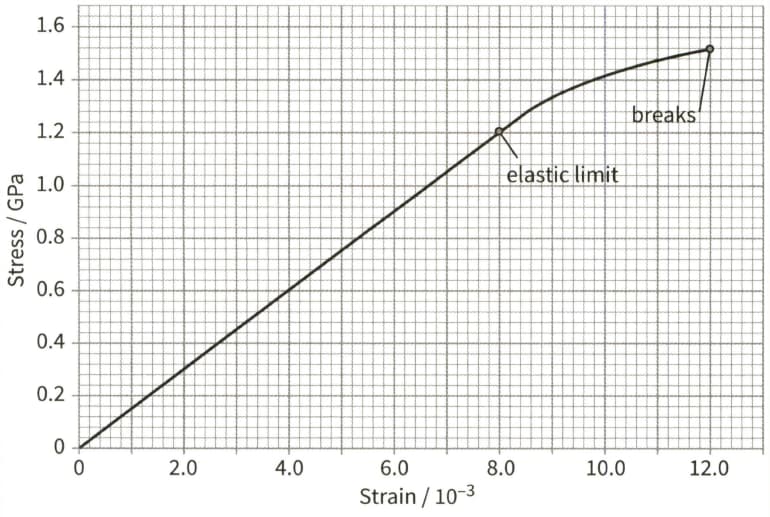
The wire has a diameter of $0.84\mathrm{mm}$ and a natural length of $3.5\mathrm{m}$. Use the graph to determine:

(d) the energy density  when the wire has a stress of 0.60GPa.

This is a force-extension graph for a spring.

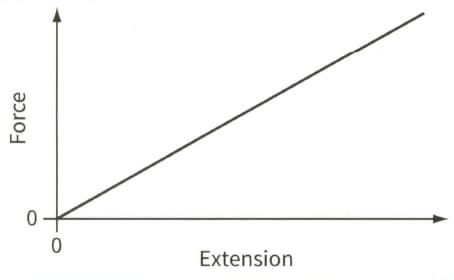
(a) State what is represented by:

(i) The gradient of the graph

This is a force-extension graph for a spring.

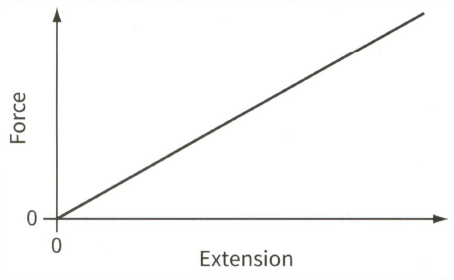
(a) State what is represented by:

(ii) The area under the graph.

This is a force-extension graph for a spring.

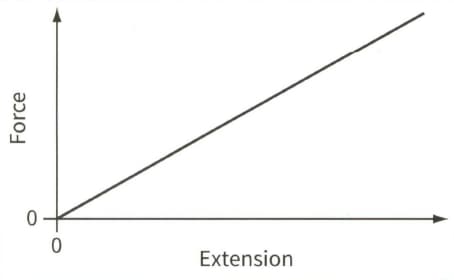
The spring has force constant $k=80{\mathrm{Nm}}^{-1}$. The spring is compressed by $0.060 \mathrm{m}$, within the limit of proportionality, and placed between two trolleys that run on a friction-free, horizontal track. Each trolley has a mass of $0.40 \mathrm{kg}$. When the spring is released the trolleys fly apart with equal speeds but in opposite directions. How much energy is stored in the spring when it is compressed by $0.060 \mathrm{m}$ ?

This is a force-extension graph for a spring.

(b) The spring has force constant $k=80{\mathrm{Nm}}^{-1}$. The spring is compressed by $0.060 \mathrm{m}$, within the limit of proportionality, and placed between two trolleys that run on a friction-free, horizontal track. Each trolley has a mass of $0.40 \mathrm{kg}$. When the spring is released the trolleys fly apart with equal speeds but in opposite directions.

(ii) Explain why the two trolleys must fly apart with equal speeds.

This is a force-extension graph for a spring.

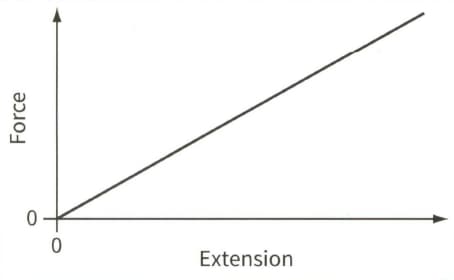
(b) The spring has force constant $k=80{\mathrm{Nm}}^{-1}$. The spring is compressed by $0.060 \mathrm{m}$, within the limit of proportionality, and placed between two trolleys that run on a friction-free, horizontal track. Each trolley has a mass of $0.40 \mathrm{kg}$. When the spring is released the trolleys fly apart with equal speeds but in opposite directions.

(iii) Calculate the speed of each trolley.