Two isolated, concentric conducting spherical shells have radii and uniform charges and , and negligible thicknesses. What is the magnitude of the electric field at radial distance , and ? With at infinity, what is at , , , , and ? Sketch and .

Important Questions on Electric Potential
Two metal spheres, each of radius , have a centre-to-centre separation of . Sphere has charge and sphere has charge . Assume that the separation is large enough for us to say that the charge on each sphere is uniformly distributed (the spheres do not affect each other). With at infinity, calculate the potential at the point halfway between the centres and the potential on the surface of sphere and sphere .
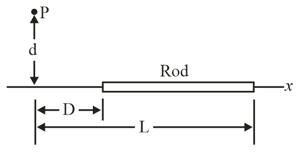
A graph of -component of electric field as a function of , in a region of space, is shown in the figure. The scale of the vertical axis is set by . The and components of electric field are zero in this region. If the electric potential at the origin is , what is the electric potential at , what is the greatest positive value of the electric potential for points on the -axis, for which , and for what value of is the electric potential zero?
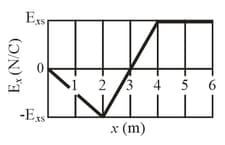
The figure shows a thin rod with a uniform charge density of . Evaluate the electric potential at the point if . Assume that the potential is zero at infinity.