What is the excess charge on a conducting sphere of radius $r=0.35 \mathrm{m}$ if the potential of the sphere is $1500 \mathrm{V}$ and $V=0$ at infinity?

The electric field in a region of space has the components $E_{\mathrm{y}}=E_{\mathrm{z}}=0$ and $E_{\mathrm{x}}=\left(4.00\right)x^2 \mathrm{N} {\mathrm{C}}^{-1}$. The point $\mathrm{A}$ is on the $y$ axis at $y=3.00 \mathrm{m}$ and the point $\mathrm{B}$ is on the $x$ axis at $x=4.00 \mathrm{m}$. What is the potential difference $V_{\mathrm{B}}-V_{\mathrm{A}}$ (in volt)?

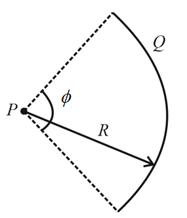
In the figure, a plastic rod which has a uniformly distributed charge $Q=-28.9 \mathrm{pC}$ has been bent into a circular arc of a radius $R=3.71 \mathrm{cm}$ and the central angle $\text{ϕ}=120°$. With $V=0$ at infinity, what is the electric potential at $P$, the centre of curvature of the rod?

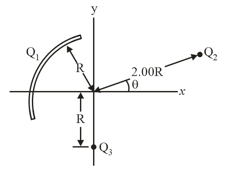
In the given figure, what is the net electric potential at the origin due to the circular arc of charge $Q_1=+7.21 \mathrm{pC}$, the two particles of charges $Q_2=4.00Q_1$ and $Q_3=-2.00Q_1$? The arc's centre of curvature is at the origin and its radius is $R=2.00 \mathrm{m}$, the angle indicated is $\text{θ}=35.0°$. What is the net electric potential at the origin if both $Q_1$ and $R$ are doubled?

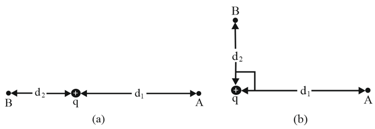
Consider a particle with charge $q=3.0 \mathrm{nC}$, point $A$ at distance $d_1=2.0 \mathrm{m}$ from $q$ and the point $B$ at distance $d_2=1.0 \mathrm{m}$. If $A$ and $B$ are diametrically opposite to each other as in the figure, (a) what is the electric potential difference $V_{\mathrm{A}}-V_{\mathrm{B}}$? (b) what is the electric potential difference if $A$ and $B$ are located as in the figure (b)?

The electric potential at points in an $xy$ plane is given by, $V=\left(2.00 \mathrm{V} {\mathrm{m}}^{-2}\right)x^2-\left(3.00 \mathrm{V} {\mathrm{m}}^{-2}\right)y^2$. What are,

(a) the magnitude and (b) the angle (relative to $+x$) of the electric field at the point $(4.00 \mathrm{m}\text{,} 2.00 \mathrm{m})$?

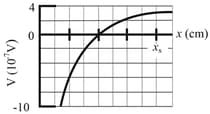
Two charged particles are shown in figure. (a) Particle $1$, with charge $q_1$, is fixed in place at distance $d$. Particle $2$, with charge $q_2$, can be moved along the $x$-axis. Figure (b) gives the net electric potential $V$ at the origin due to the two particles as a function of the $x$-co-ordinate of particle $2$. The scale of the $x$-axis is set by, $x_{\mathrm{s}}=16.0 \mathrm{cm}$. The plot has an asymptote of $V=5.92\times {10}^{-7} \mathrm{V}$ as $x\to \infty$. What is $q_2$ in terms of $e$?

                 $\left(\mathrm{a}\right) \left(\mathrm{b}\right)$                              

An infinite non-conducting sheet has a surface charge density, $\text{σ}=+5.80 \mathrm{pC} {\mathrm{m}}^2$.

(a) How much work is done by the electric field due to the sheet if a particle of charge, $q=+1.60\times {10}^{-19} \mathrm{C}$ is moved from the sheet to a point $P$ at distance, $d=6.15 \mathrm{cm}$ from the sheet?

(b) If the electric potential $V$ is defined to be $-5.00 \mathrm{mV}$ on the sheet, what is $V$ at $P$?