Calculation of Density of Unit Cell

Calcium crystallizes in a face centred cubic unit cell with a $\text{=}\text{0}\text{.560}\text{nm}\text{.}$  The density of the metal if it contains 0.1% schottky defects would be:

Copper crystallises in a face-centred cubic lattice and has a density of  $8.930\mathrm{g}{\mathrm{cm}}^{-3}$ at $393 \mathrm{K}.$ The radius of a copper atom is:
[Atomic mass of$\mathrm{Cu}=63.55\mathrm{u},{\mathrm{N}}_{\mathrm{A}}=6.02\times {10}^{23}{\mathrm{mol}}^{-1}]$

Iron has a body-centered cubic unit cell of cell edge $286.65 \mathrm{pm}$. The density of iron is $7.87 \mathrm{g} {\mathrm{cm}}^{-3}$. The Avogadro number is

(Atomic mass of iron $=56\hspace{0.17em}\mathrm{g}\hspace{0.17em}{\mathrm{mol}}^{-1}$)

X-rays diffraction studies show that copper crystallizes in an FCC unit cell with cell edge of  $3.6885\times {10}^{-8}\mathrm{cm}.$ In a separate experiment, copper is determined to have a density of  $\text{8}{\text{.92g/cm}}^{\text{3}}$, the atomic mass of copper would be:

In face-centred cubic $\left(\mathrm{FCC}\right)$ and body centred cubic $\left(\mathrm{BCC}\right),$ whose unit cell lengths are $3.5$ and $3.0$ $\mathrm{\AA }$ respectively, a metal crystallises into two cubic phases. What is the ratio of densities of $\mathrm{FCC}$ and $\mathrm{BCC}?$

A unit cell of sodium chloride has four formula units with an edge length of the unit cell $0.564 \mathrm{nm}$. What is the density of sodium chloride?

A compound AB has rock salt type structure. The formula weight of AB is 6.023 Y amu, and the closest AB distance is $Y^{\frac{1}{3}}$ nm, where Y is an arbitrary number. The density of lattice is

The density of mercury is 13.6 g ml^-1. The approximate diameter of an atom of mercury assuming that each atom is occupying a cube of edge length equal to the diameter of the mercury atom is

Copper crystallizes in an FCC unit cell with cell edge of  $3.608\times {10}^{-8}\mathrm{cm}.$ The density of copper is  $\mathrm{8}.92 \mathrm{g}/{\mathrm{cm}}^{\mathrm{3}}$, Calculate the atomic mass of copper.

Ice crystallises in a hexagonal lattice. At the low temperature at which the structure was determined, the lattice constants were $\mathrm{a}=4.53 \mathrm{\AA }$ and $\mathrm{c}=7.41 \mathrm{\AA }$. How many ${\mathrm{H}}_2\mathrm{O}$ molecules are contained in a unit cell? The density of ice is $0.92 \mathrm{g}/\mathrm{cc}$ at $0 °\mathrm{C}.$ A unit cell of ${\mathrm{H}}_2\mathrm{O}$ is shown below:

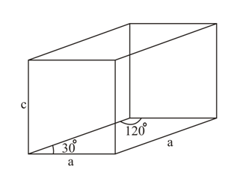
Iron exhibits $\mathrm{BCC}$-structure at room temperature. Above $500°\mathrm{C},$ it transforms to $\mathrm{FCC}$-structure. Find the ratio of the density of iron at room temperature to that at $500°\mathrm{C}.$ (Assume the atomic radii and the molar mass of iron remain constant even with variation in temperature)

If each edge of a cubic unit cell of an element having atomic mass $120$ and density $6.25 \mathrm{g}.{\mathrm{cc}}^{-1}$ measures $400 \mathrm{pm}$, then the crystal lattice is

$\mathrm{Al}$ (atomic weight $26.98$) crystallizes in the cubic system with $\mathrm{a} = 4.05 \mathrm{\AA }$. Its density is $2.7 \mathrm{g} \mathrm{per} {\mathrm{cm}}^3$. Determine the cell type. Calculate the radius of $\mathrm{Al}$atom.

Zinc selenide$\left(\mathrm{ZnSe}\right)$ crystallizes in a face-centred cubic unit cell and has a density of $5.267 \mathrm{g}/\mathrm{cc}.$ Calculate the edge length of the unit cell.

Give the answer as the nearest integer.

An unknown metal is found to have a density of $10.2 \mathrm{g}/\mathrm{cc}$ at $25°\mathrm{C}$. It is found to crystallize in a body-centered cubic lattice with a unit cell edge length of $3.147 \mathrm{\AA }$. Calculate the molar mass of the metal in grams.

Give your answer as the nearest integer.

Metallic rhodium crystallizes in a face-centered cubic lattice with a unit-cell edge length of $3.803 \mathrm{\AA }$ Calculate the molar volume ($\mathrm{in} {\mathrm{cm}}^3$) of rhodium including the empty spaces. (Give answer after rounding off to the nearest integer value.)

The unit cell of copper corresponds to a face centered cube of edge length $3.596 \mathrm{\AA }$ with one copper atom at each lattice point. The calculated density of copper in $\mathrm{kg}/{\mathrm{m}}^3$ is _________. [Molar mass of $\mathrm{Cu}=63.54 \mathrm{g}$; Avogadro's number $=6.022\times {10}^{23}$] (Round off answer to nearest integer value).

An element with molar mass $2.7\times {10}^{-2} \mathrm{kg} {\mathrm{mol}}^{-1}$ forms a cubic unit cell with edge length $405 \mathrm{pm}$. If its density is $2.7\times {10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$, the radius of the element is approximately $\times {10}^{-12} \mathrm{m}$ (to the nearest integer).

An element crystallizes in a structure having $\mathrm{fcc}$ unit cell of an edge $200 \mathrm{pm}$. Calculate the density in $\mathrm{g}/\mathrm{cc}$, if $200 \mathrm{g}$ of this element contains $5\times {10}^{24}$  atoms.

The density of iron crystal is $8.54 \mathrm{g} {\mathrm{cm}}^{–3}$. If the edge length of unit cell is $2.8 \mathrm{\AA }$ and atomic mass is $56 \mathrm{g} {\mathrm{mol}}^{–1}$, find the number of atoms in the unit cell. (Given: Avogadro’s number = $6.022 \times {10}^{23}, 1 \mathrm{\AA } = 1 \times {10}^{-8} \mathrm{cm}$)