Raoult's Law

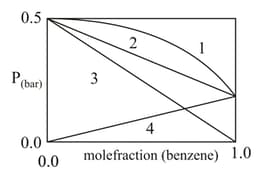
For a binary ideal liquid solution, the variation in total vapour pressure versus composition of solution is given by which of the curves?

Raoult's law becomes a special case of Henry's law when ${\mathrm{K}}_{\mathrm{H}}$$=$${\mathrm{p}}^0$. In this equation, ${\mathrm{K}}_{\mathrm{H}}$ is 

At  ${80}^{\circ }\text{C}$, the vapour pressure of pure liquid 'A' is $\text{520}\text{mm}\text{Hg}$ and that of pure liquid 'B' is $\text{1000}\text{mm}\text{Hg}\text{.}$ If a mixture solution of 'A' and 'B' boils at ${80}^{\circ }\text{C}$ and 1 atm pressure, the amount of 'A' in the mixture is:
$\left(\text{1}\text{atm}\text{=760}\text{mm}\text{Hg}\right)$

The vapour pressures of pure benzene and toluene are 160 and 60mm Hg respectively. The mole fraction of benzene is vapour phase in contact with equimolar solution of benzene and toluene is

At $100°\mathrm{C},$ benzene and toluene have a vapour pressure of $600 \mathrm{torr}$ and $1000 \mathrm{torr}$ respectively. Assuming ideal behaviour of solution, calculate the mole fraction of benzene in a solution that boils at $1 \mathrm{atm}$ and $100°\mathrm{C}$.

The vapour pressure of two pure liquids A and B, which from an ideal solution are $1000 \mathrm{and} 1600 \mathrm{torr}$ respectively, at $400 \mathrm{K}$. A liquid solution of A and B for which the mole fraction of A is $0.60$ is contained in a cylinder by a piston on which the pressure can be varied. The solution is slowly vaporised at $400 \mathrm{K}$ by decreasing the applied pressure. What is the composition of last droplet of liquid remaining in equilibrium with vapour?

A mixture of toluene and benzene forms a nearly ideal solution. Assume ${\mathrm{P}}_{\mathrm{B}}°$ and ${\mathrm{P}}_{\mathrm{T}}°$ to be the vapor pressures of pure benzene and toluene, respectively. The slope of the line obtained by plotting the total vapor pressure to the mole fraction of benzene is:

In the pressure vs. the mole fraction of benzene curves/lines shown below, the total vapour pressure of an ideal mixture of benzene and toluene will follow the curve/line.

Vapour pressure of benzene is $200 \mathrm{mm} \mathrm{Hg}$. When $2\mathrm{g}$ of non-volatile solute is dissolved in $78\mathrm{g}$ benzene, benzene solution has vapour pressure $\text{195 mm Hg}$. Calculate the molar mass of the solute in ${\mathrm{gmol}}^{-1}$( molar mass of benzene = $78{\mathrm{gmol}}^{-1}$).

Liquids $\text{'}\mathrm{A}\text{'}$ and $\text{'}\mathrm{B}\text{'}$ form an ideal solution. If the mole - fraction of $\text{'}\mathrm{A}\text{'}$ in liquid and vapour forms at equilibrium is $0.4$ and $0.6$, respectively, the value of $4\times \left(\frac{{\mathrm{P}}_{\mathrm{A}}^0}{{\mathrm{P}}_{\mathrm{B}}^0}\right)$ is:

_____ law which states that for a solution of volatile liquids, the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution.

The following is a graph plotted between the vapour pressure of two volatile liquids against their respective mole fractions.

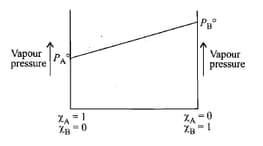
Which of the following statement is correct ?

For a dilute solution containing$2.5 \mathrm{g}$ of a non-volatile non-electrolyte solution in $100 \mathrm{g}$of water, the elevation in boiling point at $1$$\mathrm{atm}$ pressure is$2°\mathrm{C}.$ Assuming the concentration of solute is much lower than the concentration of the solvent, the vapor pressure of the solution is (${\mathrm{K}}_{\mathrm{b}} = 0.76 \mathrm{K} \mathrm{kg} {\mathrm{mol}}^{-1}$)

Two liquids $\mathrm{X}$ and $\mathrm{Y}$ form an ideal solution. At $300 \mathrm{K}$, vapour pressure of the solution containing $1$ mole of $\mathrm{X}$ and $3$ mole of $\mathrm{Y}$ is $550 \mathrm{mm} \mathrm{Hg}$. At the same temperature, if$1$  mole of $\mathrm{Y}$ is further added to this solution, vapour pressure of the solution increases by$10 \mathrm{mm} \mathrm{Hg}$ . Vapour pressure (in $\mathrm{mm} \mathrm{Hg}$) of $\mathrm{X}$ and $\mathrm{Y}$ in their pure states will be, respectively

The vapours pressure of pure components $\mathrm{X}$ and $\mathrm{Y}$ are $200$ $\mathrm{torr}$ and $100$$\mathrm{torr}$ respectively. Assuming a solution of these components obeys Raoult's law, the mole fraction of component $\mathrm{X}$ in the vapours phase in equilibrium with a solution containing equimolecular of $\mathrm{X}$ and $\mathrm{Y}$ is

Which of the following units is most useful in relating concentration of solution with its vapour pressure?

When partial pressure of solvent in solution of non-volatile solute is plotted against its mole fraction, nature of graph is

Partial pressure of solvent (mole fraction$={\mathrm{x}}_1$) in solution of non-volatile solute (mole fraction$={\mathrm{x}}_2$) is given by equation,

If Two liquids A and B which form a non-ideal solution which obey the  below equation as ${\mathrm{P}}_{\mathrm{T}}={\mathrm{P}}_{\mathrm{A}}^0+3({\mathrm{P}}_{\mathrm{B}}^0-{\mathrm{P}}_{\mathrm{A}}^0){\mathrm{X}}_{\mathrm{B}}+2({\mathrm{P}}_{\mathrm{A}}^0-{\mathrm{P}}_{\mathrm{B}}^0){\mathrm{X}}_{\mathrm{B}}^2\mathrm{.}$

Calculate the exact composition (by mole) when this mixture boils without change in composition at a definite temperature of an equimolar mixture of A and B is distilled, Where ${\mathrm{P}}_{\mathrm{A}}^0 \mathrm{and} {\mathrm{P}}_{\mathrm{B}}^0$ , $({\mathrm{P}}_{\mathrm{B}}^0>{\mathrm{P}}_{\mathrm{A}}^0)$ are vapour pressures of A and B respectively ${\mathrm{X}}_{\mathrm{B}}=$ mole fraction of B in liquid phase

Maximum boiling azeotrope will be formed by-