Types of Thermodynamic Processes

At constant temperature, for a given mass of an ideal gas

The diagram shows the pressure $p$ and volume $V$ relationship for one cycle of operation of an engine.

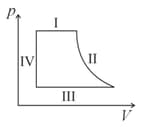
Which of the labelled parts of the cycle identify isobaric changes and adiabatic changes of state?

Work done by an ideal gas at a constant volume is__________

An isothermal process is:

The possibility of an increase in the temperature of a gas without adding heat to it happens in

If an ideal gas undergoes isothermal process from some initial state $\mathrm{i}$ to the final state $\mathrm{f},$ then the change in internal energy during this process is 

During an isothermal change, the specific heat of a gas is

What is the correct sequence in the following given graph of pressure versus volume is adiabatic reversible process?

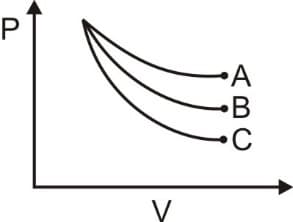
For the reversible adiabatic expansion the work done can be formulated as.

An adiabatic process occurs in which type system?

The work done in the expansion of a gas from a volume of $4 \mathrm{d}{\mathrm{m}}^3\mathrm{ }\mathrm{t}\mathrm{o}\mathrm{ }6\mathrm{ }\mathrm{d}{\mathrm{m}}^3$ against an external pressure of 3 atm is:

In the adiabatic reversible expansion of an ideal gas, the relation of pressure and volume of the gas is

The succeeding operations that enable this transformation of states are:

The work done during adiabatic reversible process is given by $w=\frac{n R\left[T_{f}-T_{i}\right]}{\gamma-1} .$ Thus, if $T_{f}>T_{i},$ then since $\gamma-1=+\operatorname{ve}(\because \gamma>1)$ the work done is + ve i.e., work is done on gas. Also if $T_{f}<T_{i}$ $w=-$ ve, thus work is done by the gas. The adiabatic process are more steeper than isothermal process and slope of adiabatic process $=\gamma \times$ slope of isothermal process $i . e .,$ slope of adiabatic process $>$ slope of isothermal process (since $\gamma>1$ ). Also the adiabatic process obey $P V^{\gamma}=$ constant, whereas in isothermal process $P V=$ constant.

The rise in temperature of an ideal gas $(\gamma=5 / 3)$, when at $27^{\circ} \mathrm{C}$ it is adiabatically reversibly compressed to $8 / 27$ of its original volume, is:

The work done during adiabatic reversible process is given by $w=\frac{n R\left[T_{f}-T_{i}\right]}{\gamma-1} .$ Thus, if $T_{f}>T_{i},$ then since $\gamma-1=+\operatorname{ve}(\because \gamma>1)$ the work done is + ve i.e., work is done on gas. Also if $T_{f}<T_{i}$ $w=-$ ve, thus work is done by the gas. The adiabatic process are more steeper than isothermal process and slope of adiabatic process $=\gamma \times$ slope of isothermal process $i . e .,$ slope of adiabatic process $>$ slope of isothermal process (since $\gamma>1$ ). Also the adiabatic process obey $P V^{\gamma}=$ constant, whereas in isothermal process $P V=$ constant.

In a thermodynamic reversible process helium gas obeys the law $\frac{T}{p^{2 / 5}}=$ constant. The heat given to a gas when temperature of $m$ moles of He is raised from $T$ to $2 T$ is:

The work done during adiabatic reversible process is given by $w=\frac{n R\left[T_{f}-T_{i}\right]}{\gamma-1} .$ Thus, if $T_{f}>T_{i},$ then since $\gamma-1=+\operatorname{ve}(\because \gamma>1)$ the work done is + ve i.e., work is done on gas. Also if $T_{f}<T_{i}$ $w=-$ ve, thus work is done by the gas. The adiabatic process are more steeper than isothermal process and slope of adiabatic process $=\gamma \times$ slope of isothermal process $i . e .,$ slope of adiabatic process $>$ slope of isothermal process (since $\gamma>1$ ). Also the adiabatic process obey $P V^{\gamma}=$ constant, whereas in isothermal process $P V=$ constant.

In a particular experiment, a gas undergoes adiabatic expansion satisfying the equation $V T^{3}=$ constant. The ratio of specific heats, $\gamma$ is:

During the process $AB$ of an ideal gas,