Addition and Subtraction of Vectors

The magnitudes of vectors  $\overrightarrow{A},\overrightarrow{B}\mathrm{and}\overrightarrow{C}$  are $3,$ $4$ and $5$ units respectively. If  $\overrightarrow{A}+\overrightarrow{B}=\overrightarrow{C}$ , then the angle between  $\overrightarrow{A}\mathrm{and}\overrightarrow{B}$  is :

Given that $\overrightarrow{P}+\overrightarrow{Q}+\overrightarrow{R}=\overrightarrow{0}.$ Two out of the three vectors are equal in magnitude. The magnitude of the third vector is $\sqrt{2}$ times that of the other two. Which of the following can be the angles between these vectors?

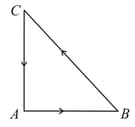
Three forces starts acting simultaneously on a particle moving with velocity $\overrightarrow{v}.$ These forces are represented in magnitude and direction by the three sides of a triangle $ABC$ (as shown). The particle will now move with velocity

Which is true about negative of a vector?

Addition of vectors is not commutative.

Which triangle is formed by the points whose position vectors are $4\overrightarrow{i}-3\overrightarrow{j}+\overrightarrow{k}, 2\overrightarrow{i}-4\overrightarrow{j}+5\overrightarrow{k}, \overrightarrow{i}-\overrightarrow{j}$?

Which triangle is formed by the points whose position vectors are $4\overrightarrow{i}-3\overrightarrow{j}+\overrightarrow{k}, 2\overrightarrow{i}-4\overrightarrow{j}+5\overrightarrow{k}, \overrightarrow{i}-\overrightarrow{j}$?

Find the square of magnitude of the vector joining two points $\left(\sin x,\cos x,1\right)$ and $\left(-\cos x,\sin x,4\right)$ in $3D$.

A vector of magnitude $5$ units along the vector $\hat{i}-2\hat{j}+2\hat{k}$ is

Let $\overrightarrow{a}=\hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}},\overrightarrow{b}=2\hat{\mathrm{i}}+2\hat{\mathrm{j}}+\hat{\mathrm{k}}$ and $\overrightarrow{c}=5\hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}}$ be three vectors. The area of the region formed by the set of points whose position vectors $\overrightarrow{r}$ satisfy the equations $\overrightarrow{r}·\overrightarrow{a}=5$  and $|\overrightarrow{r}-\overrightarrow{b}|+|\overrightarrow{r}-\overrightarrow{c}|=4$ is closest to the integer.

Find a value of $x$ for which $x(\hat{i}+\hat{j}+\hat{k})$ is a unit vector.

Find the position vectors of the points which divides internally and externally in the ratio $2:3$ the join of points $2\overrightarrow{a}-3\overrightarrow{b}$ and $3\overrightarrow{a}-2\overrightarrow{b}$.

Prove that in any $∆ABC, \cos C=\frac{a^2+b^2-c^2}{2ab}$, where a,b and c are the magnitude of the sides opposite to the vertices A, B and C, respectively.

P and Q are two points with position vectors $3\overrightarrow{a}-2\overrightarrow{b}$ and $\overrightarrow{a}+\overrightarrow{b}$, respectively. If the position vector of a point R which divides the line segment PQ in the ratio 2:1 externally is $m\overrightarrow{a}+n\overrightarrow{b}$, then $m+n=$

For given vectors, $\overrightarrow{a}=2\hat{i}-\hat{j}+2\hat{k}$ and $\overrightarrow{b}=-\hat{i}+\hat{j}-\hat{k}$ , if the unit vector in the direction of the vector $\overrightarrow{a}+\overrightarrow{b}$ is $\frac{\overrightarrow{i}+\overrightarrow{k}}{\sqrt{m}}$, then value of $m$ is

The sum of the vectors $\overrightarrow{a}=\hat{i}-2\hat{j}+\hat{k}, \overrightarrow{b}=-2\hat{i}+4\hat{j}+5\hat{k}$, and $\overrightarrow{c}=\hat{i}-6\hat{j}-7\hat{k}$ is of the form $l\hat{i}+m\hat{j}+n\hat{k}$. Find the value of $l+m+n$.

If $\overrightarrow{a}=2\hat{i}-16\hat{j}+5\hat{k}$, $\overrightarrow{b}=3\hat{i}+\hat{j}+2\hat{k}$, and $\overrightarrow{c}=l\hat{i}+m\hat{j}+n\hat{k}$ where $\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}$ denote the sides of the right-angle triangle. Then, find the value of $l+m+n$.

If $\overrightarrow{a}=(2\hat{i}-4\hat{j}+5\hat{k})$, then find the value of $k$, if $\lambda =\pm \frac{1}{k\sqrt{5}}$ so that $\lambda \overrightarrow{\mathit{a}}$ may be a unit vector.

If unit vector in the direction of the vector $\overrightarrow{c}=\hat{i}+\hat{j}+2\hat{k}$ is given as $\frac{1}{\sqrt{k}}\left(\hat{i}+\hat{j}+2\hat{k}\right)$, then find the value of $k$.