Feasible Region and Infeasible Region

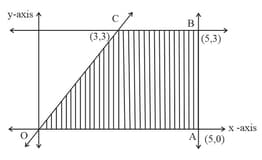
The feasible region for an $\mathrm{LPP}$ is shown shaded in the figure. Determine the maximum and minimum values of $z=x+2y$.

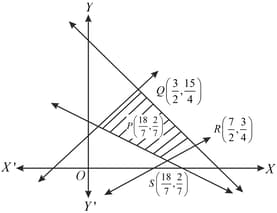
Which of the following is not a vertex of the feasible region bounded by the inequalities $2x+3y\le 6, 5x+3y\le 15$ and $x, y\ge 0$.

The feasible solution of a $\mathrm{LLP}$ belongs to

The shaded part of given figure indicates the feasible region, then the constraints are

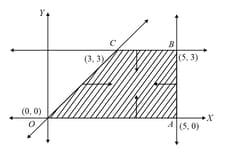
Determine the minimum value of $z=3x+2y$ (if any), if the feasible region is shown shaded in the figure.

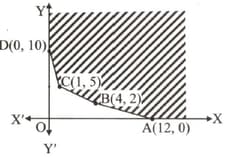
The vertex of common graph of inequalities $2x+y\ge 2$ and $x-y\le 3$, is

The shaded part of given figure indicates the feasible region



Then the constraints are

The feasible region for an $\mathrm{LPP}$ is shown shaded in the figure. Determine the maximum and minimum values of $z=x+2y$.

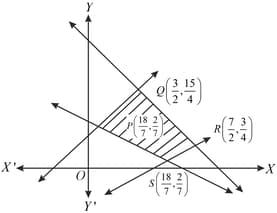
The co-ordinates of the point for minimum value of $z=7x-8y$ subject to the conditions $x+y-20\le 0, y\ge 5, x\ge 0, y\ge 0$ is

The coordinates of the corner points of the bounded feasible region are $(10,0),(2,4),(1,5)$ and $(0,8)$. the maximum of objective function $z=60x+10y$ is$\dots \dots \dots .$

The region of feasible solution under the constraints $2x+y\le 6, x\ge 0, y\ge 0$ is:

The minimum value of $Z=5x+8y$ subject to $x+y\ge 5, 0\le x\le 4, y\ge 2, x\ge 0, y\ge 0$ is

The maximum value of $Z=6x+4y$ subjected to constraints $x\le 2$, $x+y\le 3$, $-2x+y\le 1$, $x\le 0, y\le 0$ is

The maximum value of $Z=5x+7y$ subject to constraints $3x+2y\le 12, 2x+3y\le 13, x\ge 0, y\ge 0$ is

The minimum value of $P=x+3y,$ subject to the constraints $2x+y\le 20, x+2y\le 20, x\ge 0, y\ge 0$ is

The maximum value of $Z=8x+3y,$ subject to the constraints $x+y\le 3, 4x+y\le 6, x\ge 0, y\ge 0$ is 

The minimum value of the function $Z=4x+3y$ subject to the constraints $3x+2y\ge 160, 5\mathrm{x}+2y\ge 200, x+2y\ge 80, x\ge 0, y\ge 0$ is

Shaded region is represented by is

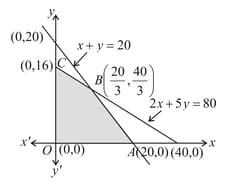
The minimum values of $z=4x+2y$ subject to the constraints $2x+3y\ge 18, x+y\le 10$ $x, y>0$ is

By graphical method, the solution of linear programming problem $\left(L.P.P.\right)$:

Maximize $Z=3x_1+5x_2$ Subject to $3x_1+2x_2\le 18, x_1\le 4, x_2\le 6$ $x_1\ge 0, x_2\ge 0$ is