Relations

Let $n\left(A\right)=m$ and $n\left(B\right)=n$, then the total number of non-empty relations that can be defined from $A$ to $B$ is:

If $n\left(A\right)=2$ and $n\left(B\right)=3$, then write the total number of non empty relations that can be defined from $A$ to $B$

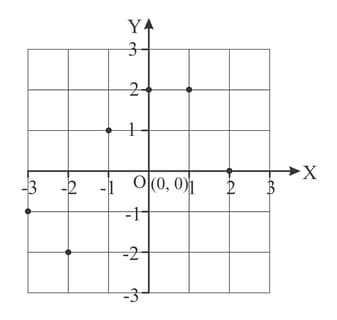
The diagram shows the graph of a relation $R$ that maps set $A$ onto set $B$.

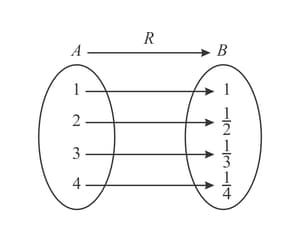
Write down $R$ as a set of ordered pairs.

Express the mapping $R$ in the form $x\to ...$

Consider the relation $\left\{\right(1,1),(1,2),(2,1\left)\right\}$. Classify it as one-to-one, many-to-one, many-to-many or one-to-many.

Consider the relation $\left\{\right(1,1),(1,2),(1,3\left)\right\}$. Classify it as one-to-one, many-to-one, many-to-many or one-to-many.

Consider the relation $\left\{\right(1,1),(2,1),(3,1\left)\right\}$. Classify it as one-to-one, many-to-one, many-to-many or one-to-many.

Consider the relation $\left\{\right(1,2),(2,3),(3,6\left)\right\}$. Classify it as one-to-one, many-to-one, many-to-many or one-to-many.

Consider the relation $\left\{\right(1,2),(2,3),(1,4\left)\right\}$. Classify it as one-to-one, many-to-one, many-to-many or one-to-many.

Let $A$ be a set consisting of $10$ elements. The number of non-empty relations from $A$ to $A$ that are reflexive but not symmetric is

Is $g=\left\{\right(1,1),(2,3),(3,5),(4,7\left)\right\}$ a function? If $g$ is described by $g\left(x\right)=\alpha x+\beta$, then what value should be assigned to $\alpha$ and $\beta$.

Let $R=\left\{\left(x,y\right):x+2y=8\right\}$  be a relation on $\mathrm{N}$. Range of $R$ is given as $\left\{a,b,c\right\}$ where $a,b,c$ are the elements of the range and $a>b>c$. Find the number $abc$.

Let $A=\{x, y, z\}$ and $B=\{1, 2\}.$ If the number of relations from $A$ to $B$ is $k$, then find the value of $k$ where $k\in$ integer.

If $R=\left\{(x,y):x^2+y^2\le 4, x,y\in \mathrm{Z}\right)$ is a relation on $\mathrm{Z} \left(\mathrm{Z} \mathrm{represents} \mathrm{an} \mathrm{integer}\right)$, then domain of $R$ is

Let $R$ be the relation from $A=\{2,3,4,5\}$ to $B=\{3,6,7,10\}$, defined by $R=$ $\{\left(x,y\right):x \text{divides} y\}$. If $R^{-1}$ is expressed in roster form, then the sum of $x$ coordinates is

If ${\mathrm{R}}_3=\left\{\right(\mathrm{x},\left|\mathrm{x}\right|\left)\right|\mathrm{x} \mathrm{is} \mathrm{a} \mathrm{real} number\}$ is a relation, If domain of given function is $R$ and range is $[a,\infty )$, then $a=$

If $A=\left\{a,b,c,d\right\}$ and $B=\left\{1,2,3\right\}$, then total number of possible relations from $A$ to $B$ is equal to

Let $A=\left\{u, v, w, z\right\}$ and $B=\{3, 5\}$$,$ then the number of relations from $A$ to $B$ is

If $A=\left\{1,2,3\right\},\mathrm{ }B=\left\{1,4,6,9\right\}$ and $R$ is a relation from $A$ to $B$ defined by $\mathrm{‘}x$ is greater than $y\text{'}$ . The range of $R$ is

If $A$ is the set of even natural numbers less than $8$ and $B$ is the set of prime numbers less than $7$, then the number of relations from $A$ to $B$ are