Operations on Sets

In a class, $20$ students opted for Physics, $17$ for Maths, $5$ for both and $10$ for other subjects. how many students are there in the class?

A survey of $100$ persons revealed that $72$ of them had eaten at restaurant P and that $52$ of them had eaten at restaurant Q. Which of the following could not be the number of persons in the surveyed group who had eaten at both P and Q?

In a certain town,$25\%$ families own a phone.$15\%$ own a car and $65\%$ own neither a phone nor a car. $2000$ families own both a car and a phone. Consider the following statements in this regard? Which of the following are the correct statements?
(I)$10\%$families own both a car and a phone.
(II)$35\%$ families own either a car or a phone.
(III) $40,000$families live in the town.

In a community of $175$ persons, $40$ read the Times, $50$ read the Samachar and $100$ do not read any. How many persons read both the papers ?

Which of the following binary operations for set $N$ are associative and/or commutative:

$\left(a\right)$  $a*b=1 \forall a,b\in N$

$\left(b\right)$  $a*b=\frac{a+b}{2} \forall a,b\in N.$

For any two sets $A$ and $B$, $A-\left(A-B\right)$ is equal to

Let $A$ be te set of non-negative integers, $I$ is the set of integers, $B$ is the set of non-positive integers, $E$ is the set of even integers and $P$ is the set of prime numbers then

An organization awarded $48$ medals in event ${}^{\text{'}}A^{\text{'}}$, $25$ in event ${}^{\text{'}}B^{\text{'}}$ and $18$ in event ${}^{\text{'}}C^{\text{'}}$. If these medals went to total $60$ men and only five men got medals in all the three events, then, how many received medals in exactly two of three events?

Let $A=\left\{0, 1, 2, 3, 4\right\}$, $B=\left\{x\in N|x\le 20\right\}$, $C=\left\{x\in N|x>3\right\}$, $D=\left\{x\in N| x \mathrm{is} \mathrm{divisible} \mathrm{by} 7\right\}$.

Determine $A\cup B$

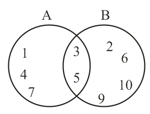
From the adjacent figure, find $n\left(A\right)$, $n\left(AUB\right)$ and $n(A\cap B)$. What is relation between $n\left(A\right), n\left(B\right), n(A\cap B)$ and $n\left(AUB\right)$?

A college awarded $38$ medals in football, $15$ in basketball and $20$ in cricket. If these medals went to a total of $58$ men and only three men got medals in all the three sports, how many received medals in exactly two of the three sports ?

If $X$ and $Y$ are two sets such that $X\cup Y$ has $50$ elements, $X$ has $28$ elements and $Y$ has $32$ elements, how many elements does $X\cap Y$ have ?

If $X=\left\{x:x^2-12x+20=0\right\}$ and $Y=\left\{x:x^2+5x-14=0\right\}$, then $X-Y=$

Suppose that in a certain exam, $200$ students appear for Mathematics, $50$ appear for physics, $100$ appear for Chemistry, $20$ appear for Mathematics & Physics, $60$ appear for Mathematics & Chemistry, $35$ appear for Physics & Chemistry, while $245$ appear for either Mathematics or Physics or Chemistry.

Determine the number of students who appear for

(i) All 3 subjects

(ii) Exactly for one of the subjects

Use Venn Diagram to find the same.

If $n\left(P\right)=12, n\left(M\right)=12$ and $n\left(M\cap P\right)=4$ then $n\left(M\cup P\right)=$

Let $A$ and $B$ be two sets such that $n\left(A-B\right)=14+x, n\left(B-A\right)=3x$ and $n\left(A\cap B\right)=x$. Draw a venn diagram to illustrate this information. If $n\left(A\right)=n\left(B\right)$, then find the value of $x$.

When $A\subset B$, then $A-B=$

Let $S=\left\{4,6,9\right\}$ and $T=\left\{9,10,11,....,1000\right\}$. If $A=\left\{a_1+a_2+a_3+...+a_k, k\in N, a_1, a_2, a_3,...., a_k\in S\right\}$, then the sum of elements in the set $T-A$ is equal to

If $P\left(A\right)=\frac{2}{3}, P\left(B\right)=\frac{2}{5}, P(A\cup B)=\frac{1}{3}$ then find $P\left(A\cap B\right)$.

If $n\left(A\cup B\right)=97,n\left(A\cap B\right)=23$ and $n\left(A-B\right)=39$, then $n\left(B\right)$ is equal to