Solution of Linear Programming Problems

For the $\mathrm{LPP}$, minimize $Z=2 x+y$ subject to $x+2y\le 10,x+y\ge 1,y\le 4$ and $x,y\ge 0$, then $Z$ is

Minimize $Z=\sum _{j=1}^{10}\sum _{i=1}^{30}{C}_{ij}·X_{ij}$
subject to
$\sum _{j=1}^{10}{X}_{ij}\le a_{i,}i=1,2,3....30$

$\sum _{i=1}^{30}{X}_{ij}\le b_{j,}j=1,2,3....10$
is a $\mathrm{LPP}$ with number of constraints

Let $X_1$ and $X_2$ are optimal solutions of a $\mathrm{LPP}$ for which objective function is maximum. Then

The co-ordinate of the point for minimum value of $Z=7x-8y$ subject to the conditions $x+y-20\le 0,y-5\ge 0,x\ge 0,y\ge 0 \mathrm{is} \left(\alpha ,\beta \right)$. Then $\alpha +\beta$ is equal to 

The minimum value of $Z=2x+3y$ subject to the constraints $2x+7y\ge 22,x+y\ge 6,5x+y\ge 10,x,y\ge 0$ is equal to 

The linear programming problem: Max $Z=x_1+x_2$ such that $2x_1-x_2\ge -1, x_1\le 2, x_1+x_2\le 3$ and $x_1,x_2\ge 0$ has

For the following feasible region, the liner constraints are

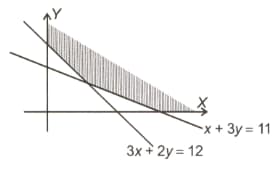
Inequation $y-x\le 0$ represents

Which of the following is not vertex of the positive region bounded by the inequalities $2x+3y\le 6, 5x+3y\le 15$ and $x,y\ge 0$ ?

Mr. Das wants to invest $\mathrm{Rs} 12000$ in Public Provident Fund $\left(\mathrm{PPF}\right)$ and in National Bonds. He has to invest at least Rs 1000 in $\mathrm{PPF}$ and at least Rs 2000 in bonds. If the rate of interest on $\mathrm{PPF}$ is $12\%$ per annum and that on bonds is $15\%$  per annum, how should he invest the money to earn maximum annual income?

Determine graphically the minimum value of the objective function $Z=-50x+20y$ subject to the constrains:

$2x-y\ge -5$

$3x+y\ge 3$

$2x-3y\le 12$

$-5x+2y\ge -30$

 and $x\ge 0, y\ge 0.$

What are the theorems, which are used to solve $\mathrm{LPPs}$?

Determine the maximum value of $Z=9x+y$, If the feasible region for a $\mathrm{LPP}$ is shown in the figure given below 

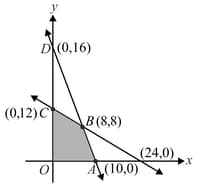
Detrmine the minimum value of $Z=3x+2y$ (If any) if the feasible region for a $\mathrm{LPP}$ is shown in the figure.

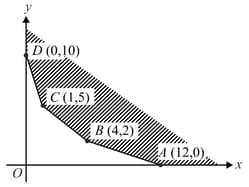
Determine the maximum value of $z=4x+3y$, If the feasible region for a $\mathrm{LPP}$ is shown in the figure, given below. 

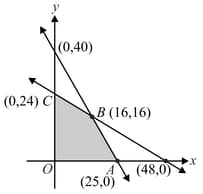
Feasible region (shaded) for a $\mathrm{LPP}$ is shown in the figure given below. If $Z=4x+3y$ be the objective function, then find the point, where minimum of $Z$ occurs.

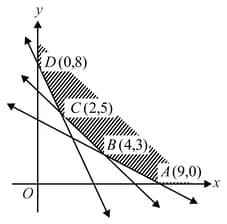
The corner points of the feasible region determined by the system of linear constraints are $\left(0,10\right),\left(5,5\right),\left(15, 15\right), \left(0,20\right)$. Let $Z=p x+q y$, where $p, q>0$. Find the condition on $p$ and $q$ so that the maximum of $Z$ occurs at both the points $\left(15,15\right)$ and $\left(0,20\right)$.

Corner points of the feasible region for an $\mathrm{LPP}$ are $\left(0,2\right),\left(3,0\right)\left(6,0\right),\left(6,8\right) \mathrm{and} \left(0,5\right)$.

If $F=4x+6y$ be the objective function, then find the points or region where minimum value of $F$ occurs.

The feasible region for an $\mathrm{LPP}$ is shown in the figure given below

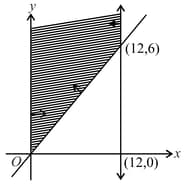
Let $P=3x-4y$ be the objective function. Then find the minimum value of $P$.

The feasible region for an $\mathrm{LPP}$ is shown in the figure given below

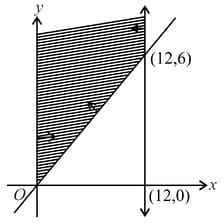
Let $P=3x-4y$ be the objective function. Then find the maximum value of $P$.