Interaction between Two Circles

Two circles touch each other internally. The radii of these circles are $2 \mathrm{cm}$  and $3 \mathrm{cm}$ respectively. Find the length of the largest chord of the outer circle which touches the internal circle at a point?$$

The radius of the circle, having centre at (2, 1), whose one of the chord is a diameter of the circle ${\text{x}}^2+{\text{y}}^2-2\text{x}-6\text{y}+6=0$

If the circle  $C_1:x^2+y^2=16$ intersects another circle $C_2$ of radius $5$ in such a manner that the common chord is of maximum length and has a slope equal to  $\frac{3}{4}$ , then the coordinates of the centre of $C_2$ are

The number of common tangents, to the circles $x^2+y^2-18x-15y+131=0$ and $x^2+y^2-6x-6y-7=0$, is 

Consider the circles $x^2+y^2-13x-15y+13=0 \text{and} x^2+y^2-6x-6y-7=0$ then number of common tangents are:

The incentre of the triangle formed by common tangents of circles $x^2+y^2-8x=0$ and $x^2+y^2+2x=0$

Consider two circles $C_1:{\left(x-1\right)}^2+{\left(y-4\right)}^2-16=0$ and $C_2:{\left(x-13\right)}^2+{\left(y-9\right)}^2-81=0$. If a circle of radius $r$ touches $x-$axis and $C_1$ and $C_2$ externally, then $r$ is equal to

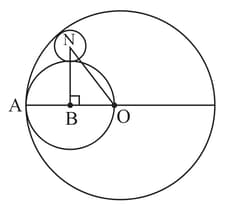
In the figure given below with centre $O$, and another circle with centre at the mid-point $B$ of the radius $OA$ and passing through $O$. A small circle is drawn as shown, tangent to both the larger circles such that its centre $N$ is directly above $B$(that is $BN\perp AB$). If the perimeter of the triangle $NBA$ is $8$ cm, find the value in $cm$, of the radius of the small circle.

Three circles $C_3, C_2, C_1$ of radius $3, 6, 9$ respectively touch as shown in figure. A chord $AB$ to circle $C_1$ touch circle $C_2 \& C_3$.

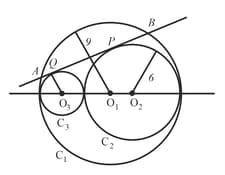
The length of chord $AB$ is $\alpha \sqrt{14}$ and length of common tangent $PQ$ is $\beta \sqrt{2}$, then number of divisors of $\left(3^{\beta -1}-2^{\alpha -1}\right)$ is

Two circles of radii $8$ and $4$ touch each other externally at a point $A$. A point $B$ is taken on larger circle through which a straight line is drawn touching the smaller$$ circle at $C$. If $AB=\sqrt{6}$, find $BC$.

If the circles $a{x}^2+a{y}^2+2bx+2cy=0$ and $A{x}^2+A{y}^2+2Bx+2Cy=0$ touch each other then

If the common chord of the circles $x^2+y^2+4y=0$ and $x^2+y^2-4x-5=0$ is the diameter of the circle $S=0$ then the abscissa of the centre of the circle $S=0$ is

If the circles ${\mathrm{C}}_1:x^2+y^2+2x+4y-20=0, {\mathrm{C}}_2:x^2+y^2+6x-8y+9=0$ have $n$ common tangents and the length of the tangent drawn from the centre of similitude to the circle $C_2$ is $l$ then $\frac{l}{n^2}=$

If $\left(0,\frac{3}{4}\right)$ is the radical centre of the circles $S\equiv x^2+y^2+\alpha x+6y=0,S^{\text{'}}\equiv x^2+y^2+2\alpha x+\alpha y+6=0$ and $S^{"}\equiv x^2+y^2+6\alpha x-\alpha y+3=0$ then the distance between the radical centre and the centre of the circle $S^{\text{'}}=0$ is

If $\theta$ is the angle between the circles $x^2+y^2-2x-4y-4=0$ and $x^2+y^2-8x-12y+43=0$ then $\left|7\sec \theta -18\cos \theta \right|=$

The equation of the transverse common tangent of the circles $x^2+y^2-6x-8y+9=0$ and $x^2+y^2+2x-2y+1=0$ is

The image of the point $\left(3,4\right)$ with respect to the radical axis of the circles $x^2+y^2+8x+2y+10=0$ and $x^2+y^2+7x+3y+10=0$ is

Which of the following statements is true about circle $x^2+y^2+2x=0$ and $x^2+y^2-6x=0$

Consider three circles :

$C_1:x^2+y^2=r^2$

$C_2:{\left(x-1\right)}^2+{\left(y-1\right)}^2=r^2$

$C_3:{\left(x-2\right)}^2+{\left(y-1\right)}^2=r^2$

If a line $L:y=mx+c$ be a common tangent to $C_1,C_2$ and $C_3$ such that $C_1$ and $C_3$ lie on one side of line $L$ while $C_2$ lies on other side, then the value of $20\left(r^2+c\right)$ is equal to 

The circles $S=0$ cuts the circles $C_1=x^2+y^2-8x-2y+16=0$ and $C_2=x^2+y^2-4x-4y-1=0$ orthogonally. If the common chord of $S=0$ and $C_1=0$ is $2x+13y-15=0$ then the centre of $S=0$ is