Straight Line and its Equations

If the line $y-\sqrt{3}x+3=0$ cuts the parabola $y^2=x+2$ at $A$ and $B$, then find the value of $PA·PB$. (where, $P\equiv \left(\sqrt{3},0\right)$)

If the line $y-\sqrt{3}x+3=0$ cuts the parabola $y^2=x+2$ at $A$ and $B$, then find the value of $PA·PB$. (where, $P\equiv \left(\sqrt{3},0\right)$)

A straight line cuts off the intercepts $OA=a$ and $OB=b$ on the positive direction of $x-$axis and $y-$axis respectively. If the perpendicular from origin to this line makes an angle $\frac{\mathrm{\pi }}{6}$ with positive direction of $y-$axis and are of $∆OAB$ is $\frac{98}{3}\sqrt{3}$ sq. units, then $a^2-b^2$ is equal to

The equation of the straight line with gradient $1$, passing through $\left(\frac{m}{2},\frac{n}{2}\right)$ where, $m,n\in R$ satisfies the equation ${\sec }^{2}n\left(m+2\right)+m^2=1$, where, $n\in \left[-\frac{\mathrm{\pi }}{2},\frac{\mathrm{\pi }}{2}\right]$ is

The equation of the line which is $10$ units from the origin and the normal ray from the origin to it makes an angle $\frac{\mathrm{\pi }}{4}$ with positive direction of $x-$axis measured in the clockwise direction is

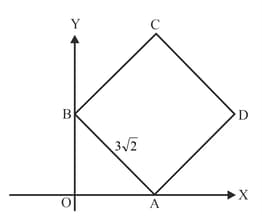
Find the equations of the lines $OA, OB, AB, BD \& AD$ from the given figure in which $AOB$ is the right-angled isosceles triangle and $ABCD$ is a square of side length $3\sqrt{2}$ units.

The parametric equation of a line is $x=-2+\frac{r}{\sqrt{10}}$ and $y=1+\frac{3r}{\sqrt{10}}$, then for the line

Find the equation of straight line passing through $\left(-a,0\right)$ and making the triangle with axes of area '$T$'.

If the slope of the line $\left(\frac{x}{a}+\frac{y}{b}-1\right)+k\left(\frac{x}{b}+\frac{y}{a}-1\right)=0$ is $-1$, then the value of '$k$' is

In a triangle $ABC$ vertex $A$ is the point $\left(-4,5\right)$. Its altitudes are $AD,BE$ and $CF$. The coordinates of the points $D,E,F$ are respectively $\left(\frac{16}{5},\frac{-23}{5}\right),\left(4,1\right)$ and $\left(-1,-4\right)$. The coordinates of the other vertices of the triangle are

The coordinate of the midpoints of the sides of a triangle $ABC$ are $\left(6,-1\right),\left(-1,-2\right)$ and $\left(1,-4\right)$. Find the length and equations of it's sides.

A line makes an intercept of $5$ and $4$ on the $x$-axis & $y$-axis respectively. If the axes are rotated about the origin by an angle a such that the length of intercept on the new $x$-axis is $8$. The length of intercept on the new $y$-axis, is

The equation of the line passes through $\left(2,3\right)$ ant which is farthest from $\left(0,0\right)$ is

Use concept of slope to prove following points are collinear.

$\left(0,2\right),\left(1,5\right),\left(-2,-4\right) \& \left(-6,-16\right)$

Use concept of slope to prove following points are collinear.

$\left(4,2\right),\left(5,4\right),\left(2,-2\right) \& \left(3,0\right)$

Use concept of slope to prove following points are collinear.

$\left(4,8\right),\left(5,12\right),\left(9,28\right) \& \left(11,36\right)$

Use concept of slope to prove following points are collinear.

$\left(5,-2\right),\left(4,-1\right),\left(1,2\right) \& \left(3,0\right)$