Various Forms of the Equation of a Line
Various Forms of the Equation of a Line: Overview
This topic consists of various concepts like x-intercept and y-intercept of a Line,Equation of Straight Line in Various Forms,Equation of Straight Line in Point Slope Form, etc.
Important Questions on Various Forms of the Equation of a Line
The equation of a straight line passing through the intersection of the lines , and through the point .
In the gradient-intercept form of equation , the point where line cuts -axis is:
The equation of the image of the line with respect to is
If a line passes through point and has gradient then the equation will be:
A line cuts the x-axis at and the y-axis at B A variable line PQ is drawn perpendicular to AB cutting the x-axis in P and y axis in Q. If AQ and BP intersect at R, find the locus of R.
A vertex of an equilateral triangle is and equation of the opposite side is Find the equation of the other sides of the triangle.
Find the equation of a straight line which is parallel to the line and passes through the point
If and are perpendicular, then equal to:
If the point lies on the curve traced by the mid-points of the line segments of the lines between the co-ordinates axes, then is equal to
A straight line cuts the co-ordinate axes at and If the mid-point of is find the equation of
A straight line cuts off the intercepts and on the positive direction of axis and axis respectively. If the perpendicular from origin to this line makes an angle with positive direction of axis and are of is sq. units, then is equal to
A straight line cuts the co-ordinate axes at and . If the midpoint of is , find the equation of .
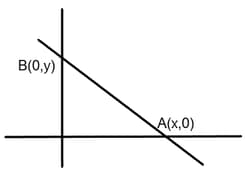
A straight line cuts the co-ordinate axes at and . If the midpoint of is , find the equation of .
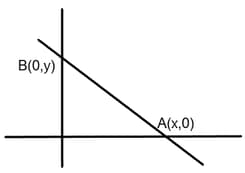
Write the equation of the lines for which , where is the inclination of the line and -intercept is .
Show that two lines and , where are perpendicular if .
Equation of a line is . Find its -and -intercepts.
Consider a parallelogram whose sides are represented by the lines and . The equation of the diagonal not passing through the origin is
The slope of a line joining the points and is then find
Find the equation of the normal to the curve at the point . if slope of tangent is .
If the triangle with vertices and , then the equation of median from is
