Using Tree Diagrams to Show Outcomes

Author:Karen Morrison & Nick Hamshaw
Upper Secondary: IGCSE
IMPORTANT

Using Tree Diagrams to Show Outcomes: Overview

In this topic, we will learn to calculate the probability through tree diagrams and the steps to draw the same. The rules for calculating possible events like independent, mutually exclusive events, etc., are included along with some exercises.

Important Questions on Using Tree Diagrams to Show Outcomes

MEDIUM
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 1

A bag contains 12 beads. Five are red and the rest are white. Two beads are drawn at random. The first bead is replaced before the second is drawn.Represent the possible outcomes on a tree diagram. Find both beads are red and both beads are white.

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 2

A bag contain eight blue marbles and two red marbles . Two marbles are drawn at random. The first marble is replaced before the second is drawn.What is the probability of getting two red marbles.

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 3

An unbiased coin is tossed twice. Draw a tree diagram to show the outcomes and use it to find the probability of the two tosses giving the same result.

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 4

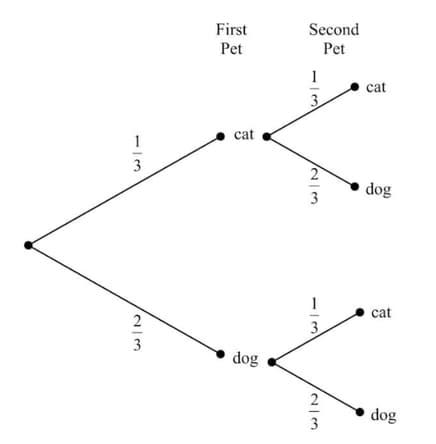
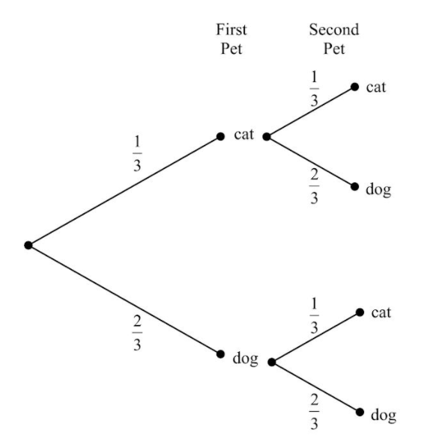
Harold wants to buy two new pets; he will buy them a week apart. He prefers dogs to cats, but only slightly, and decides that so long as he buys them as puppies and/or kittens, it doesn't matter what combination he gets. The tree diagram below represents what combination of two pets he might buy. What is the probability that he buys two cats?

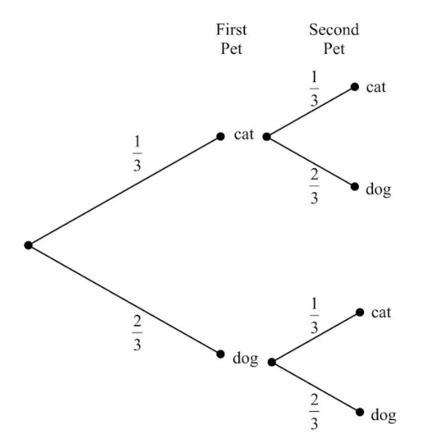
Question Image

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 5

Harold wants to buy two new pets; he will buy them a week apart. He prefers dogs to cats, but only slightly, and decides that so long as he buys them as puppies and/or kittens,it doesn't matter what combination he gets. The tree diagram below represents what combination of two pets he might buy. What is the probability that he buys a cat and a dog?

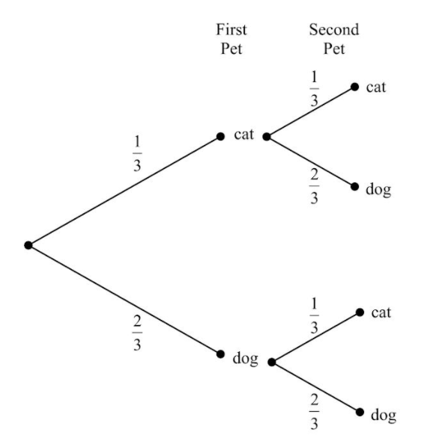
Question Image

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 6

Harold wants to buy two new pets; he will buy them a week apart. He prefers dogs to cats, but only slightly, and decides that so long as he buys them as puppies and/or kittens, it doesn't matter what combination he gets. The tree diagram below represents what combination of two pets he might buy. How many possible combinations of pet could be buy?

Question Image

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 7

A bag contain eight blue marbles and two red marbles . Two marbles are drawn at random. The first marble is replaced before the second is drawn.What is the probability of getting two blue marbles.

MEDIUM
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 8

A bag contain eight blue marbles and two red marbles . Two marbles are drawn at random. The first marble is replaced before the second is drawn.What is the probability of getting one red marble and one blue marble. ( Write answer in simplest form.)

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 9

Harold wants to buy two new pets; he will buy them a week apart. He prefers dogs to cats, but only slightly, and decides that so long as he buys them as puppies and/or kittens, it doesn't matter what combination he gets. The tree diagram below represents what combination of two pets he might buy. Based on the probabilities, what combination is he most likely to buy?

Question Image

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 10

A bag contain eight blue marbles and two red marbles . Two marbles are drawn at random. The first marble is replaced before the second is drawn. Draw a tree diagram to show all possible outcomes.

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 11

 Four cards marked A, B, C and D are in a container. A card is drawn, the letter noted, and then it is replaced. Another card is then drawn and the letter noted to make a two-letter combination. What is the probability of getting the letter combination BD?

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 12

Four cards marked A, B, C and D are in a container. A card is drawn, the letter noted, and then it is replaced. Another card is then drawn and the letter noted to make a two-letter combination. How many outcomes are in the sample space?

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 13

Four cards marked A, B, C and D are in a container. A card is drawn, the letter noted, and then it is replaced. Another card is then drawn and the letter noted to make a two-letter combination. Draw a tree diagram to show the sample space in this experiment.

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 14

Sandra has a bag containing three coloured counters: red, blue and green. How many outcomes do not contain the blue counter? 

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 15

Sandra has a bag containing three coloured counters: red, blue and green. How many outcomes contain at least one blue counter?

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 16

Sandra has a bag containing three coloured counters: red, blue and green. How many outcomes produce two counters the same colour?

EASY
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 17

Sandra has a bag containing three coloured counters: red, blue and green. How many possible outcomes are there for the two draws?

MEDIUM
IMPORTANT
Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition>Data Handling>Probability Using Tree Diagrams and Venn Diagrams>Using Tree Diagrams to Show Outcomes> Q 18

Sandra has a bag containing three coloured counters: red, blue and green.Draw a tree diagram to show the possible outcomes when one Counter is drawn from the bag at random, then returned to the bag before another counter is drawn at random.