Altitude of a Triangle

A triangle and a parallelogram are constructed on the same base such that their areas are equal. If the altitude of the parallelogram is $100 \mathrm{m}$, then the altitude of the triangle is?

In $∆\mathrm{ABC}$, $\angle A<\angle B$, the altitude to the base divides vertex angle $C$ into two parts $C_1$ and $C_2$ adjacent to $BC$, then which one of the relation can be obtained?

In triangle $\mathrm{PQR},\mathrm{PS}$ is the altitude to $\mathrm{QR}$. Which of the following must be true?

The point $"H"$ in the given triangle $ABC$ is

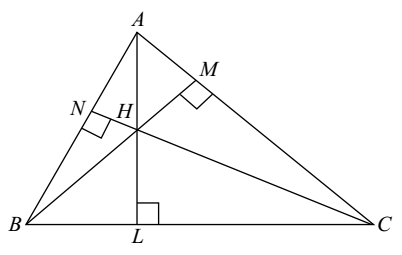
Orthocentre is a

The point of intersection of the altitudes of a triangle is

The number of altitudes of a triangle is

The orthocenter of a right-angled triangle is formed

The orthocentre of an acute angled triangle is

The orthocentre of an obtuse angled triangle is

The orthocentre of a triangle is determined by

What is the maximum number of points at which three coplanar non-concurrent lines can intersect?

Consider the following statements regarding concurrent lines:

$\left(i\right)$. Only lines can be concurrent

$\left(ii\right)$. Parallel lines can not be concurrent lines.

$\left(iii\right)$. Two concurrent lines share a common intersection point.

Which of the above statements are correct?

Observe the following figure:

The characteristics of point $M$ is as follows:

$\left(i\right)$. Intersection point

$\left(ii\right)$. Collinear point

$\left(iii\right)$. Point of concurrency

Now, which are the statement is true about point $M$?

Derive the formula for altitude of an isosceles triangle.

Define altitude of a triangle. Write its properties.

The orthocentre of a right-angled triangle lies outside the triangle.

The orthocentre of an obtuse-angled triangle lies outside the triangle.

The orthocentre of an acute-angled triangle lies outside the triangle.

Which is true? Three lines are concurrent if they have only