Perpendicular from the Center of a Circle to a Chord

$C$ is the centre of the circle whose radius is $10 \mathrm{cm}$. Find the distance of the chord from the centre if the length of the chord is $12 \mathrm{cm}$.

In figure, $O$ is the centre of the circle of radius $5 cm$. $OP\perp AB$, $OQ\perp CD$, $AB\parallel CD, AB=6 cm$ and $CD=8 cm$. Determine the length of $PQ$.

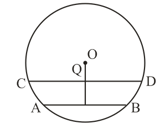
Two parallel chords, $AB$ and $CD$are $3.9 \mathrm{cm}$ apart and lie on the opposite sides of the centre of a circle. If the length of $AB$ is $1.4 \mathrm{cm}$ and the length of $CD$ is $4 \mathrm{cm}$, find the radius.

The perpendicular distance of a chord from the centre of a circle is $6 \mathrm{cm}$. If the length of the chord is $2 \mathrm{cm}$ less than thrice the perpendicular distance, what is the radius of the circle?

In the given figure, seg. $\mathrm{AB}$ is a diameter of a circle with centre $\mathrm{P}$. $\mathrm{C}$ is any point on the circle. $\mathrm{CE}\perp \mathrm{AB}$. Prove that $\mathrm{CE}$ is geometric mean of $\mathrm{AE}$ and $\mathrm{EB}$. Write the proof with the help of following steps.

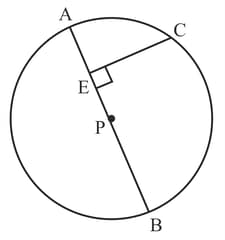
(a) Draw ray $\mathrm{CE}$ to intersect the circle at $\mathrm{D}$.

(b) Show that $\mathrm{CE}=\mathrm{ED}$.

(c) Write the result using theorem of intersection of chords inside the circle.

(d) Using $\mathrm{CE}=\mathrm{ED}$, complete the proof.

Let $M$ be the middle point of the chord $PQ$ of a circle. If $AB$ be any other chord through $M$ then prove that $PQ<AB$.

The two circles with centres $X$ and $Y$ intersect each other at the points $A$and $B$. $A$is joined with the mid-point$\text{'}S\text{'}$of $XY$ and the perpendicular on $SA$ through the point $A$ is drawn which intersects the two circles at the points $P$ and $Q$. Let us prove that $PA=AQ$.

$AB$ and $PQ$ are parallel chords of a circle centered at $O$. If distance between $AB$ and $PQ$ is $7 \mathrm{cm}$, radius of circle is $25 \mathrm{cm}$ then area$\left(ABQP\right)$ is equal to:

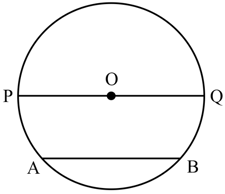
The length of a chord which is at a distance of $4 \mathrm{cm}$ from the centre of a circle of radius $6 \mathrm{cm}$ will be-

In the given circle, with centre $O$, $\mathrm{K} \mathrm{and} \mathrm{L}$ are the mid-points of equal chords $\text{AB and CD}$ respectively. $\angle OLK=25°$, then the value of $\angle LKB$ is equal to

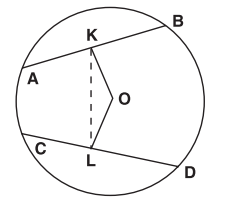
Two parallel chords $AB \text{and} CD$ in a circle are of lengths $8 \mathrm{cm} \text{and} 12 \mathrm{cm}$, respectively and the distance between them is $6 \mathrm{cm}$. The chord $EF$, parallel to $AB \text{and} CD$ and midway between them is of length $\sqrt{k}$, where $k$ is equal to:

AB and CD are two parallel chords of a circle of radius $3$ cm. If the length of AB is $4$ cm and CD is $5$ cm, then the distance between them is (in cm)?

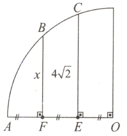
O is centre of quarter circle. If AF=FE=EO then x =?

OABC is a square inscribed in a quarter circle with O as centre. Then tan $\alpha$ is ?

The centres of two circles with radii $8$ cm and $3$ cm are $13$ cm apart. A direct common tangent touches the circles at A and B respectively, then the length of AB is ?

In the given figure, $AB=8 \mathrm{cm}, OP=3 \mathrm{cm}$. The radius (in cm) of the circle is equal to

Two concentric circles of radii $a$ and $b$, $(a>b)$ are given. If a chord of the larger circle is drawn such that it touches the smaller circle and the length of this chord is equal to $k\sqrt{a^2-b^2}$, then the value of $2k$ is equal to

If $PQ=12 \mathrm{cm}, OP=10 \mathrm{cm}$, then the length of $OM$ is

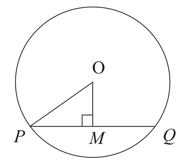
In the given figure, $\mathrm{CD}$ is the perpendicular bisector of the chord $\mathrm{AB}.$If $\mathrm{AB}=2 \mathrm{cm}, \mathrm{CD}=4 \mathrm{cm}$ and the radius of the circle is $r \mathrm{cm}$, then find the value of $r$ in decimal.

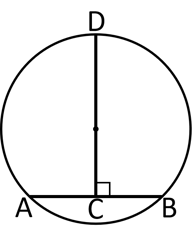
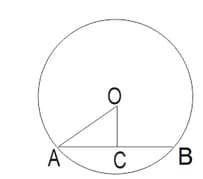
In the above figure $O$ is the center of the circle. Select the following statements as true and false : $\left(\mathrm{i}\right)$ $\mathrm{AC}=\mathrm{CB}$ $\left(\mathrm{ii}\right)$ $AB=\frac{1}{2}AC$ $\left(\mathrm{iii}\right)$ $AB=2AC$ $\left(\mathrm{iv}\right)$ $OC=\sqrt{O{A}^2-A{C}^2}$ $\left(\mathrm{v}\right)$ $AC=\sqrt{O{A}^2+O{C}^2}$