Chord Properties of Circles

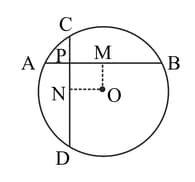
In the figure given below two equal chords $AB$ and $CD$ of a circle with centre $O$ intersect at right angles at $P.$ If $M$ and $N$ are mid-points of the chords $AB$ and $CD$ respectively, prove that $NOMP$ is a square.

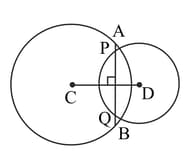
In the figure given below $C$ and $D$ are centres of two intersecting circles. The line $APQB$ is perpendicular to the line of centres $CD.$ Prove that

$\left(\mathrm{i}\right) AP=QB \left(\mathrm{ii}\right) AQ=BP$

In the adjoining figure, $O$ is the centre of the circle. If $OA= 5 \mathrm{cm}, AB= 8 \mathrm{cm} \text{and} OD\perp AB$, then length of $CD$ is equal to:

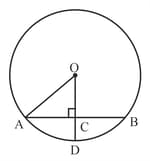
$AD$ is diameter of a circle and $AB$ is a chord. If $AD= 34 \mathrm{cm} \text{and} AB= 30 \mathrm{cm}$, then the distance of $AB$ from the centre of circle is

$ABC$ is an isosceles triangle inscribed in a circle. If  $AB= AC=12\sqrt{5} \mathrm{cm}$ and $BC= 24 \mathrm{cm}$. Find the radius of the circle.

In the given figure, $AD$ is a diameter of a circle. If the chord $AB$ and $AC$ are equidistant form its centre $O$, prove that $AD$ bisects $\angle BAC$ and $\angle BDC$.

In the figure $\left(\mathrm{ii}\right)$given below, $P$ is a point of intersection of two circles with centres $C$ and $D$. if the straight line $APB$ is parallel to $CD$, prove that $AB=2CD.$

In the figure $\left(\mathrm{i}\right)$given below, two circles with centres $C, D$ intersect in points $P, Q.$ if length of common chord is $6$cm and $CP=5$cm, $DP=4$cm, calculate the distance $CD$ correct to two decimal places.

A chord of length $48$ cm is at a distance of $10$cm from the centre of a circle. If another chord of length $20$cm is drawn in the same circle, find its distance from the centre of the circle.

The radii of two concentric circles are $17$cm and $10$ cm; a line$PQRS$ cuts the larger circle at $P$ and $S$ and the smaller circle at $Q$ and $R$ . If $QR=12$ cm, calculate $PQ$.

In the figure $\left(\mathrm{ii}\right)$ given below, $AB$ and $CD$ are equal chords of a circle with $\left(\mathrm{i}\right) AE=CE$ $\left(\mathrm{ii}\right) BE=DE$

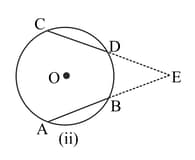
In the figure $\left(\mathrm{i}\right)$ given below, $AD$ is a diameter of a circle with centre $O.$ If $AB \parallel CD$ , prove that 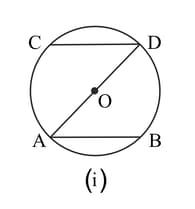$AB=CD.$

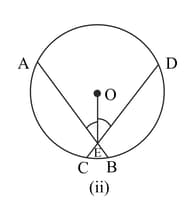
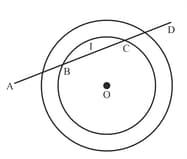
In the figure $\left(2\right)$ given below, chords $AB$ and $CD$ of a circle with centre $O$ intersect at $E.$  If $OE$ bisects $\angle AED$, prove that $AB=CD.$

In the figure given below, a line $l$ intersects two concentric circles at the points $A,B,C \& D.$,Prove that $AB=CD.$.

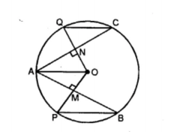
In the figure given below, $O$ is the centre of a circle. If $AB$ and $AC$ are chords of the circle such that $AB=AC$ and$OP\perp AB, OQ\perp AC$, prove that $PB=QC$.

In the figure given below, $OD$ is perpendicular to the chord $AB$ of a circle whose centre is $O$. If $BC$ is a diameter, show that $CA=2OD.$

In an equilateral triangle, prove that the centroid and the circumcentre of the triangle coincide.

If a diameter of a circle is perpendicular to one of two parallel chords of the circle, prove that it is perpendicular to the other and bisects it.

The line joining the mid-points of two chords of a circle passes through its centre. Prove that the chords are parallel.

The length of the common chord of two intersecting circles is $30 \mathrm{cm}$. If the radii of the two circles are $25 \mathrm{cm} \text{and} 17 \mathrm{cm}$, find the distance between their centres.