Definition of Circle

A chord distant $2 \mathrm{cm}$ from the centre of a circle is $18 \mathrm{cm}$ long. If the length of a chord of the same circle which is $6 \mathrm{cm}$ distant from the centre is $k cm$ then find the value of $k$.

The radius of a circle is $2.5 \mathrm{cm}$. $\mathrm{AB}$ and $\mathrm{CF}$ are two parallel chords  $3.9 \mathrm{cm}$apart. If, $\mathrm{AB}=1.4 \mathrm{cm}$, find $\mathrm{CF}$.

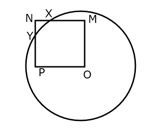
In Figure $\mathrm{OMNP}$ is a square. A circle drawn with centre $O$ cuts the square in $X$ and $Y$. Prove that: $∆\mathrm{OXM}\cong ∆\mathrm{OYP}$, Hence prove that $\mathrm{NX}=\mathrm{NY}$.

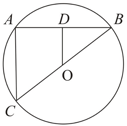
In the given Figure $\mathrm{OD}$ is perpendicular to the chord $AB$ of a circle whose centre is $O$. Prove that $\mathrm{CA}=2\mathrm{OD}$.

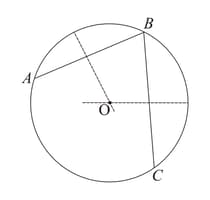
Find the centre of a given circle.

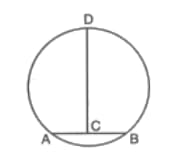
In the given Figure, $\mathrm{CD}$ is the perpendicular bisector of the chord $\mathrm{AB}.$If, $\mathrm{AB}=2 \mathrm{cm} \mathrm{and} \mathrm{CD}=4 \mathrm{cm}$, if the radius of the circle is $k cm$ then find the value of $k$ in decimal.

In the figure, $\mathrm{AB}=8 \mathrm{cm}, \mathrm{CM}=1 \mathrm{cm}$, $\mathrm{CM}$ is the perpendicular bisector of $\mathrm{AB},$ radius $\mathrm{OA}=x\mathit{ }\mathrm{cm}$. Find $x$.

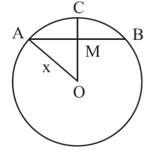
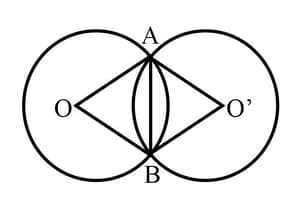
The length of the common chord of two equal intersecting circles is $10 \mathrm{cm}$ and the distance between the two centres is $6 \mathrm{cm}$, if the radius of each circle is $k.83 cm$ then find the value of $k$.

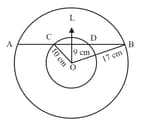
In figure, circles are concentric with Centre $O$. If the length of $\mathrm{AC}$ is $k cm$, then find the value of $k$ in decimal. 

.

In a circle of radius $5 \mathrm{cm}$, $\mathrm{AB}$ and $\mathrm{CD}$ are two parallel chords of length $8 \mathrm{cm}$ and $6 \mathrm{cm}$ respectively.If the distance between the chords, when they are on the opposite side of the centre is $k \mathrm{cm}$, find the value of $k$

In a circle of radius $5 \mathrm{cm}$, $\mathrm{AB}$ and $\mathrm{CD}$ are two parallel chords of length $8 \mathrm{cm}$ and $6 \mathrm{cm}$ respectively.

If the distance between the chords is $k cm$ then find the value of $k$, if they are on the same side of the centre.

In figure, $\mathrm{CD}$ is diameter which meets the chord $\mathrm{AB}$ in $\mathrm{E},$ such that $\mathrm{AE}=\mathrm{BE}=4 \mathrm{cm}$, If $\mathrm{CE}$ is $3 \mathrm{cm}$, then the radius of the circle is $r \mathrm{cm}$. Find the value of $r$ correct to one decimal place.

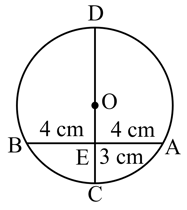
In the figure, the radius of the given circle with, centre $\mathrm{C},$ is $6 \mathrm{cm}$. If the chord $\mathrm{AB}$ is $3 \mathrm{cm}$ away from the centre and its length is $k \mathrm{cm}$, then find the value of $k$, correct to one decimal place. [Take $\sqrt{3}=1.7$]

If the length of a chord which is at a distance of $12 \mathrm{cm}$ from the centre of a circle of radius $13 \mathrm{cm}$ is $k \mathrm{cm}$, then find the value of $k$.