Alternate Segment and its Angles
Alternate Segment and its Angles: Overview
This Topic covers sub-topics such as Alternate Segment Theorem, Tangent Segment Theorem, Tangent Secant Segment Theorem, Converse of Tangent Theorem, Converse of Alternate Segment Theorem and, Theorem on Angle between Tangent and Secant
Important Questions on Alternate Segment and its Angles
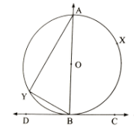
A circle passes through the vertices of a . The line and the tangent to the circle at meet in . If find .
In the given figure, is a kite inside the circle given below, and are the tangents to the circle at and respectively. If , then the value of is
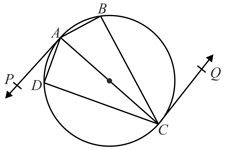
Prove Theorem of angle between tangent and secant for the following diagram
How can you prove the converse of the above theorem. "If a line in the plane of a circle is perpendicular to the radius at its end point on the circle, then the line is tangent to the circle " .
Prove that a parallelogram circumscribing a circle is a rhombus.
State and prove converse of alternate segment theorem
If line is a secant of the circle where points are on the circle and the line is such that it touches the circle at point , and where point is in the corresponding alternative segment then line is not tangent to the circle at point .
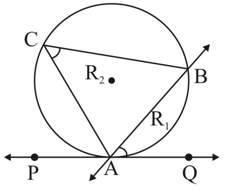
In the above diagram is a secant, is a tangent. The value of is , is . The value of is .

In the above diagram is a secant, is a tangent. The value of is , is . Find the value of .
In the diagram, is a chord and meets a diameter at . and . Find and .

Find the value of in the given diagram:

According to the converse of alternate segment theorem "If a line is drawn through an end point of a _____ of a circle so that the angle formed with the chord is equal to the angle subtended by the chord in the alternate segment, then the line is a tangent to the circle"
According to the converse of alternate segment theorem "If a line is drawn through an end point of a chord of a circle so that the angle formed with the chord is equal to the angle subtended by the chord in the alternate segment, then the line is a "
If be an angle with the vertex that lies on a circle with the centre . Line is a secant of the circle that intersects the circle at the point . Line is a tangent at the point . Point is the interior of the angle . Point is the exterior of the angle . Then
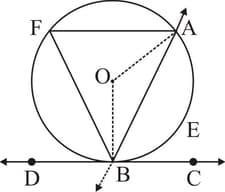
If line is a secant of the circle where points are on the circle and the line is such that it touches the circle at point , and _____ where point is in the corresponding alternative segment then line is tangent to the circle at point .
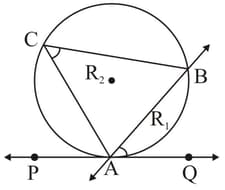
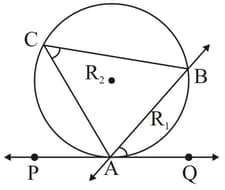
If line is a secant of the circle where points are on the circle and the line is such that it touches the circle at point , and where point is in the corresponding alternative segment then
From an external point , and are tangents to a circle with centre . If , then the value of is
Let be a trapezium in which and . Suppose has an incircle which touches at and at . Given that and find
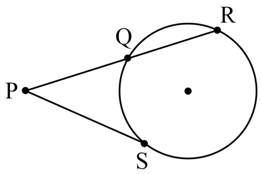
Suppose are two unequal circles; and are the direct common tangents to these circles. A transverse common tangent cuts in and in . If units, then is -
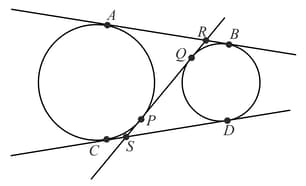
Tangents to a circle at points and on the circle intersect at a point . If units and units, then the radius of the circle is