Number of Tangents from a Point on a Circle

Prove that the point $(1, - 1)$ lies within the circle $x^2 + y^2 - 4x + 6y + 4 = 0.$

Find the position of the point $\left(2,3\right)$  with respect to the circle $x^2+y^2-6x-4y=0$.

Find the position of the point $\left(3,4\right)$  with respect to the circle $x^2+y^2=9$

Find the position of the point $\left(5,12\right)$  with respect to the circle $x^2+y^2=169.$

How many tangents can you draw to a circle from a point outside the circle at a fixed distance?

The number of tangents to a circle drawn from a point outside the circle is:

In the given figure, $TA$ and $TB$ are tangents to the circle with centre $\text{'}O\text{'}$. If $\mathit{\angle }ATB=80°$, then $\mathit{\angle }ABT=?$

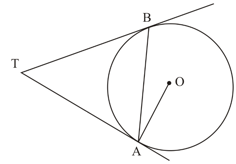
In the given figure, $\mathrm{O}$ is the centre of the circle and $\mathrm{AB}=15 \mathrm{cm}$ and $\mathrm{AC}=7.5 \mathrm{cm}$. If the radius of the circle is $r \mathrm{cm}$, then find the value of $r$.

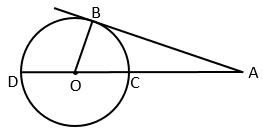
The radius of a circle is $8 \mathrm{cm}$. If the length of a tangent drawn to this circle from a point at a distance of $10 \mathrm{cm}$ from its centre is $k \mathrm{cm}$, then find the value of $k$.

In the given figure, tangent $\mathrm{PT}=12.5 \mathrm{cm}$ and $\mathrm{PA}=10 \mathrm{cm},$ find $\mathrm{AB}.$

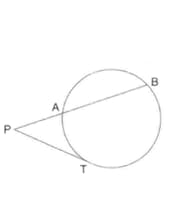
In the given figure, two circles touch each other externally at point $\mathrm{P}$. $\mathrm{AB}$ is the direct common tangent of these circle prove that tangent at point $\mathrm{P}$ bisect $\mathrm{AB}$.

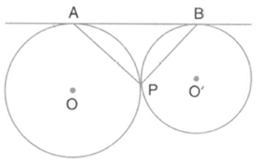
In the figure, if $\mathrm{AB}=\mathrm{AC}$ then prove that $\mathrm{BQ}=\mathrm{CQ}$. 

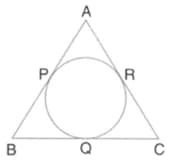
From the given figure, prove that $\mathrm{AP}+\mathrm{BQ}+\mathrm{CR}=\mathrm{BP}+\mathrm{CQ}+\mathrm{AR}.$ Also, show that $\mathrm{AP}+ \mathrm{BQ} +\mathrm{CR} =\frac{1}{2}\times \text{perimeter of}△\mathrm{ABC}$.

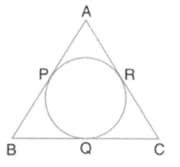
If the sides of a parallelogram touch a circle, prove that the parallelogram is a rhombus. 

Two circle touch each other internally. Show that the tangent drawn to the two circle from any point on the common tangent, are equal in length. 

Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
 

In the figure, chords $\mathrm{AE}$ and $\mathrm{BC}$ intersect each other at point $\mathrm{D}.$

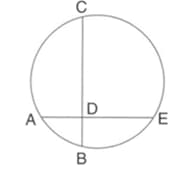
If $\mathrm{AD}=\mathrm{BD},$ show that $\mathrm{AE}=\mathrm{BC}.$
 

In the given figure, diameter $\mathrm{AB}$ and chord $\mathrm{CD}$ of a circle meet at $\mathrm{P}.$ $\mathrm{PT}$ is a tangent to the circle at $\mathrm{T}.$ $\mathrm{CD}=7.8 \mathrm{cm}, \mathrm{PD}=5 \mathrm{cm}, \mathrm{PB}=4 \mathrm{cm}.$ Find $\mathrm{AB}$ and the length of tangent $\mathrm{PT}.$

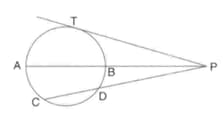
In the given figure, two circles touch each other externally at point $\mathrm{P}. \mathrm{AB}$ is the direct common tangent of these circles Prove that angle $\mathrm{APB} = 90°.$
 

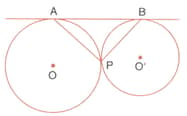
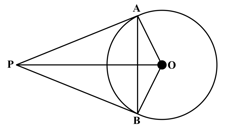
In the figure below, centre of the circle is $O$and tangents $PA \text{and} PB$ drawn from point $P$touch the circle at $A$ and $B$ respectively. Prove that$OP$ is the bisector of line $AB$.