Criteria for congruence of triangles
Criteria for congruence of triangles: Overview
This topic covers the criteria for congruence of triangles. The congruence criteria for the triangles are SSS (Side-Side-Side) criteria, SAS criteria, and ASA Criteria.
Important Questions on Criteria for congruence of triangles
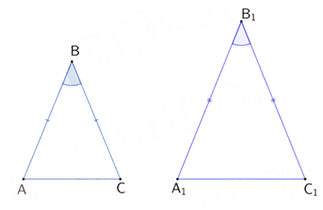
If the above two isosceles triangles are congruent and if , then find .
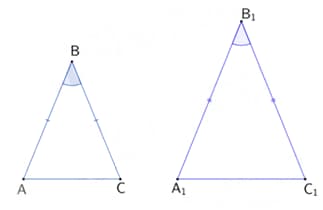
If the above two isosceles triangles are congruent and if , then find .
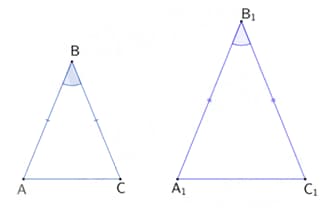
If the above two isosceles triangles are congruent and if , then find .
If the equal sides and the angle included between the equal sides of the triangles are equal to each other, then .
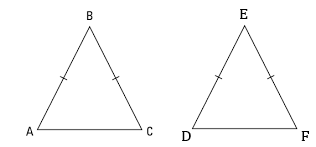
If the equal sides and the angle included between the equal sides of the triangles are equal to each other, then prove that .
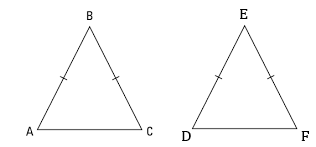
If the equal sides and the angle included between the equal sides of the triangles are equal to each other, then prove that .
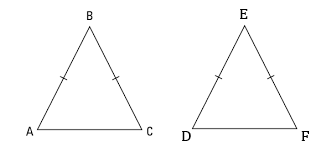
Prove that any two isosceles triangles are congruent if the equal sides and the angle included between the equal sides of the triangles are equal to each other?
If their sides are equal to each other in the two right-angled isosceles triangles given, then .
In the two right-angled isosceles triangles, prove that if their sides (other than the hypotenuse) are equal to each other?
In the two right-angled isosceles triangles, prove that if their sides (other than the hypotenuse) are equal to each other?
Prove that any two right-angled isosceles triangles are congruent if their sides are equal to each other?
What is congruence among the right-angled isosceles triangles?
In the figure, line segments and bisect each other at . Is ?
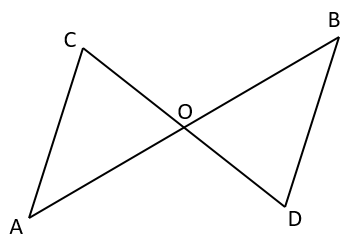
In the given pair of triangles, parts bearing identical marks are congruent. State the test by which triangles are congruent.
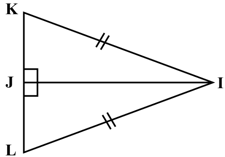
State True or False:
Two equilateral triangles are always congruent.
Sheela drew a triangle whose dimensions were x cm, y cm and z cm.
Meena drew a triangle whose dimensions were exactly half that of Sheela’ triangle.
Leela said both triangles followed the SSS rule of congruency as they were exactly proportional.
Reena pointed out that they were similar and not congruent.
Tina gave a solution to make the triangles congruent.
Pick the right option.
Which value of x will prove ∆ ABC ≌ ∆ DEF by SSS postulate?
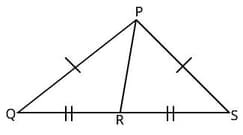
Martha outlined the shape of a triangle where side PQ and side PR measure 4 ft each. If S is the midpoint of QR, is ∆ PQS ≌ ∆PRS?
In ∆ PQR and ∆ PSR, PQ = PS and QR = SR. What is a third criterion so that the two triangles are congruent?
If we prove ∆ XYZ ≌ ∆ PQR by SSS congruence rule that means: