Special Cases of Construction of Quadrilateral
Special Cases of Construction of Quadrilateral: Overview
This topic covers concepts such as Construction of a Quadrilateral when Four Sides and One Angle are Given, Necessary Conditions for Construction of Unique Quadrilateral, Necessary Conditions for Construction of Unique Rhombus, etc.
Important Questions on Special Cases of Construction of Quadrilateral
A quadrilateral in which and are perpendicular to each other, is a _____. (Kite/Rhombus/Parallelogram)
and these five measurements are sufficient to construct a quadrilateral : _____ (yes/no)
A _____ cannot be constructed with the data of the three angles alone, the measurements of the two included sides are also required.
Are these five measurements sufficient to draw a unique quadrilateral in which and ? (Write answer as Yes or No)
Steps of construction of a rhombus, whose one side is and a diagonal is equal to are given below.
Step : Mark the points of intersection of arcs above asand below as.
Step : Withas a centre, draw arcs of above and below of .
Step : Draw .
Step : Join and .
Step : With as the centre, draw arcs of above and below of .
Identify the correct order of construction of the Rhombus.
It is possible to construct a quadrilateral with one side and three angles.
A quadrilateral in which cm and cm are perpendicular to each other is a _____ . (Square/Rhombus/Parallelogram)
It is possible to construct a square having cm.
If a quadrilateral has cm and the diagonals intersecting at then it is a rectangle.
Which type of quadrilateral is formed by using following measurements:
A quadrilateral with having cm and cm.
A diagonal of a quadrilateral is a line segment that joins two _____ vertices of the quadrilateral. (Opposite/Adjacent)
To construct a quadrilateral minimum number of elements required are _____.
Which type of quadrilateral is obtained by measurements given below:
A quadrilateral with
Which type of quadrilateral is obtained by following measurements?
Quadrilateral in which and .
Can you draw a parallelogram where , and ? (Yes/No)
Suppose the two diagonals of a Rhombus are equal in length. Which quadrilateral do you obtain?
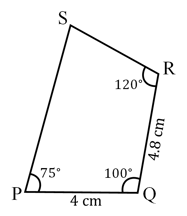
Can you construct the below quadrilateral (rhombus) by taking as a base instead of ? (Yes/No)
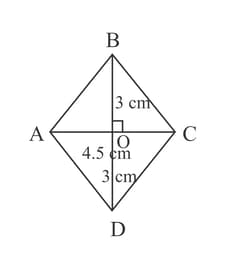
Can you construct the below quadrilateral by taking as base instead of ? (Yes/No)
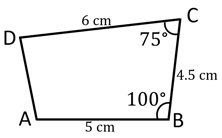
Can you construct the quadrilateral if , , , and . (yes/no)
Can you construct the above quadrilateral , if we have an angle of at instead of . [Yes / No]