Area of a Triangle

The area in the square unit of the triangle is formed by the graphs of $x = 4$, $y = 4$ and $3x+4y = 12$.

Find the area of the quadrilateral whose vertices are taken in order formed by $\left(-4, -2\right), \left(-3,-5\right), \left(3, -2\right), \left(2, 3\right)$

Show that the points $(-2, 5), (6, -1) \text{and} (2, 2)$ are collinear.

How to determine the area of a triangle when the three points are given?

Find the value of $K$ if $A\left(2,3\right), B\left(4,K\right), C\left(6,-3\right)$ if the points are collinear.

Find the area of the ABC with $A\left(1,-4\right)$ and mid-points of the sides through $\text{'}A\text{'}$ being $\left(2, -1\right)$ and $\left(0, -1\right)$.

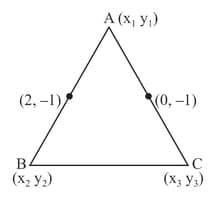
The area of $∆PQR$ is $4$ square units. The coordinates of $P$ and $Q$ are $\left(-2,2\right)$ and $\left(-3,2\right)$ respectively. The point $R$ lies on the line $y+3x=4$. Find the coordinates of $R$

Plot the roots of the equations $x^2-4x+3=0$ and $2y^2-7y+3=0$ and find the area of the smallest triangle formed by joining these points and origin.

Let $A\left(1, 1\right), B\left(-4, 3\right), C\left(-2, -5\right)$be vertices of a triangle $ABC, P$ be a point on side $BC$, and ${∆}_1 \text{and} {∆}_2$ be the areas of triangle $APB\hspace{0.17em}\text{and} ABC$ respectively.

If ${∆}_1:{∆}_2= 4:7$ then the area enclosed by the lines $AP, AC$ and the $x-$axis is :

Show that $\left(a,1\right),\left(b,1\right),\left(c,1\right)$ are collinear points.

Prove that the points $\left(0, a\right), \left(\frac{b}{2}, \frac{a}{2}\right)$ and $\left(b, 0\right)$ are collinear.

Find the area of the triangle with vertices at $\left(-k+1, 2k\right)$, $\left(k, 2-2k\right)$ and $\left(-4-k, 6-2k\right)$. For what values of $k$ these points are collinear

Find the area of the triangle whose vertices are $\left(3, 8\right), \left(-4, 2\right)$ and $\left(5, 1\right)$.

The two adjacent sides of a cyclic quadrilateral are $2cm$ and $5 cm$ and angle between them is $60°$. If the area of the quadrilateral is $4\sqrt{3} sq. cm$ then the sum of the remaining two sides is _____.  

The centroid of a triangle is $\left(1, 4\right)$ and the coordinates of its two vertices are $\left(4,-3\right)$ and $\left(-9,7\right)$. Then the area of the triangle is  

Find the area of triangle $ABC$ whose vertices are $A\left(2,2\right),B\left(3,4\right)$ and $C\left(-1,3\right)$.

Find the area of a pentagon with the coordinates at $A(0,4),B(3,2),C(3,-1),D(-3,-1)$ and $E(-3,2)$

Find the area of $∆ABC$ Whose vertices are $A(10, -6), B(2, 5)$ and $C(-1, 3).$

If points $\left(a,0\right)$, $\left(0,b\right)$ and $\left(1,1\right)$ are collinear, then the value of $\left(\frac{1}{a}+\frac{1}{b}\right)$ is

If the vertices of a triangle are $(1,2), (4, -6) \text{and} (3,5)$ then