Section Formula

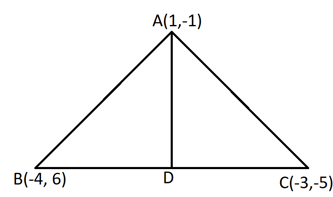
In the given figure AD is the median of $△ABC$. Find the coordinates of point $D$.

Using the section formula, prove that the three points $\left(-4, 6\right)$, $\left(2, 4\right)$ and $\left(8, 2\right)$ are collinear.

If $\mathrm{P}(5,6)$ is the mid-point of the line segment joining $\mathrm{A}(6,5)$ and $\mathrm{B}(4,\mathrm{y})$, then find $\mathrm{y}$.

In the figure, the midpoints of the large quadrilateral are joined to form the small quadrilateral within:

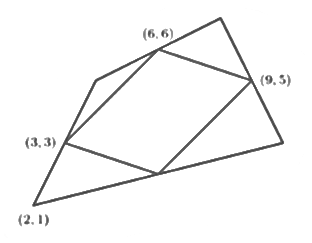
Find the coordinates of the other three vertices of the larger quadrilateral?

Find the ratio in which the line $3x+y=9$ divides the line segment joining the points $\left(1,3\right)$ and $\left(2,7\right)$.

In what ratio, point $\left(7, 6\right)$ divides the line joining the points $\left(11, 8\right)$ and $\left(1, 3\right)$.

If midpoints of sides of a triangle is $(1,2),(0,-1)$ and $(2,-1),$ then find its vertices.

Find the co-ordinates of point which trisects the line joining point $(11,9)$and $(1,2)$.

If point $P(3, 5)$ divides line segment which joins $A(-2, 3)$ and $B(x, y)$ in the ratio $4: 7$internally, then find the co-ordinates of $B$.

Find the midpoint of line joining the points $(22, 20)$ and $(0,16)$.

Find the coordinates of the point which divides the line segment joining the points $(5, -2)$ and $\left(-1\frac{1}{2}, 4\right)$ in the ratio $7: 9$ externally.

Find the ratio where point $(-3, p),$ divides internally the line segment which joins points $(-5,-4)$ and $(-2,3)$ . Also find $p$.

Find the coordinates of the point which quartersects the line joining point $(-4,0)$ and $(0,6)$.

Prove that midpoint of a line segment which joins points $(5, 7)$ and $(3, 9)$ is the same as midpoint of line segment which join points $(8,6)$ and$(0,10)$.

Prove that midpoint $\left(C\right)$ of hypotenuse in a right-angled triangle $AOB$ is situated at equal distance form vertices $O, A$ and $B$ of triangle.

If coordinates of one end and the midpoint of a line segment are $(4,0)$ and $(4,1)$ respectively, then find the coordinates of other ends of the line segment. 

Find the ratio in which point $( 3,4 )$ divides the line segment which joins points $(1,2)$ and $(6,7)$.

Find the ratio in which line $3x+y=9$ divides the line segment which joins points $(1, 3)$ and $(2, 7)$.

In which ratio, the point $(11,15)$ divides the line segment joining points $(15,15)$ and $(9,20)$?
 

In which ratio, $y$-axis divides the line segment which joins points $(2, -3)$ and $(5, 6)$?