Concurrent Lines in Triangles
Concurrent Lines in Triangles: Overview
This Topic covers sub-topics such as Concurrency of Altitudes of Triangle, Concurrency of Two External and One Internal Angle Bisectors of Triangles, Concurrency of Perpendicular Bisector of Sides of Triangle and, Concurrency of Medians of Triangle
Important Questions on Concurrent Lines in Triangles
The point of two external angle bisector for any side of a triangle and internal angle bisector of the angle opposite side chosen is called
The point of intersection of the bisectors of the angles of any triangle is called
The circumcentre is defined as:
The point of intersection of the perpendicular bisectors of the sides of a triangle is called:
In an obtuse - angled triangle, the obtuse angled is . Find the angle made on its orthocentre.
If the coordinates of the mid-points of the sides of a triangle are and . Find its centroid.
Name the triangle for which centroid, circumcentre, orthocentre and incentre coincide with each other.
Where does the orthocentre lie in the case of an acute-angled triangle?
Where does the orthocentre lie in the case of an obtuse-angled triangle?
Where does the orthocentre lie in the case of a right angled triangle?
In triangle , is a median and and , find the value of .
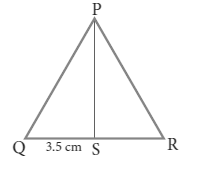
In figure, point is the point of concurrence of the medians of . If , find the lengths of .
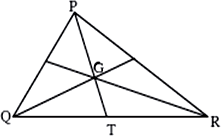
In the median and passes through the point . If then, find .
In the median and passes through the point . If then find (in ) (correct up to one decimal place)
Find in how many points do the three medians of a triangle meet.
