Equivalent Versions of Euclid's Fifth Postulate
Equivalent Versions of Euclid's Fifth Postulate: Overview
This topic covers concepts, such as, Euclidean Theorem for Intersection of Two Lines, Equivalent Versions of Euclid's Fifth Postulate, Significance of Euclid's Fifth Postulate, Limitations of Euclidean Geometry & Non-euclidean Geometry etc.
Important Questions on Equivalent Versions of Euclid's Fifth Postulate
Which of the following is not true?
Two lines intersect at a point . Which of the following is true for the distance between the two lines as they travel beyond point ?
Euclidean geometry is applicable for flat surfaces whereas Non-Euclidean geometry is applicable for _____surfaces.
Study the following statement:
"Two intersecting lines cannot be perpendicular to the same line".
Check whether it is an equivalent version to the Euclid's fifth postulate.
Which Euclid's postulate led to the discovery of several other geometries while attempting to prove it using other postulates and axioms.
Write whether the following statements are True or False? Justify your answer:
Attempts to prove Euclid's fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
Euclid's theorem for intersection of two lines states that two distinct lines can not have
Euclid's theorem for intersection of two lines states that two distinct lines can not have more than _____ point in common.
(Note: Write answer in words)
Two distinct lines can have more than one point in common.
Write the number of points common for two different lines.
State and prove Euclid's theorem for the intersection of two lines.
Euclid's fifth postulate does imply the existence of parallel lines.
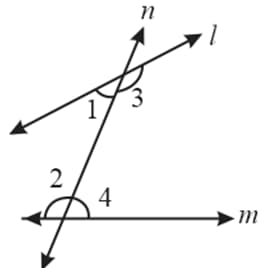
In the above figure, . If the lines and are produced indefinitely they will meet on that side on which .
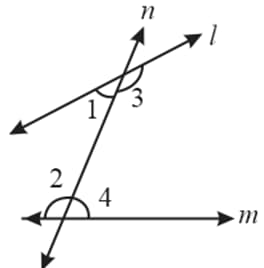
In the adjacent figure, a line falls on lines and such that the sum of the interior angle and is less than .On which side of the transversal will the line and line meet?
State Euclid's fifth postulate. Mention one significance of Euclid's fifth postulate.
Two distinct intersecting lines cannot be _____ to the same line.
Two distinct intersecting lines cannot be parallel to the same line.
For every line and for every point not lying on , there exists a unique line passing through and _____ to ..
Prove Playfair's axiom.
State Playfair’s axiom.
