Euclid's Definitions, Axioms and Postulates

The edges of a plane surface are

Number of straight lines passing through the point $\left(1,2\right)$ is

A line which lies evenly with the points on itself is called a 

Which of these following statement is true.

The edges of the surface are

"A circle can be drawn with any centre and any radius" is Euclids 

"A circle can be drawn with any centre and any radius." is Euclids

"A terminated line can be produced indefinitely." is Euclids 

Which of the following is a true statement?

The total number of propositions in the Elements are:

$\mathrm{A}$ is of the same age as $\mathrm{B}$ and $\mathrm{C}$ is of the same age as $\mathrm{B}$. Euclid's which axiom illustrates the relative ages of $\mathrm{A}$ and $\mathrm{C}$?

The number of interwoven isosceles triangles in Sriyantra is

Fill in the blanks:

A $\_\_\underline{P}\_\_$ is breadthless length. A $\_\_\underline{Q}\_\_$ is a line which lies evenly with the points on itself. A $\_\_\underline{R}\_\_$ is that which has length and breadth only. A $\_\_\underline{S}\_\_$ is a surface which lies evenly with the straight lines on itself.

Choose the correct option:

It is known that if $a+b=10$, then $a+b-c=10-c$. State the Euclid's axiom that best illustrates this statement.

Quantities which are equal to the same quantity are equal to each other. The whole is equal to the sum of its parts and hence, whole is greater than the parts.

If in a line segment $AE, AB=BC, BC=CD$ and $CD=DE$, then $AB=$

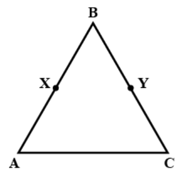
In the given figure, $AC=XD$, $C$ is mid-point of $AB$ and $D$ is mid-point of $XY$. Using an Euclid's axiom, we have

For every line $l$ and for every point $P$ (not on $l$ ), there does not exist a unique line through $P$

In the given figure, if $AB=BC$ and $BX=BY$, then

Priya and Pooja have the same amount of money. If each gets $₹ 4000$ more, how will their new amounts be compared?

Euclid's axiom $5$ is