Angle sum property of a Triangle

Two equilateral triangles on a straight line are shown below.

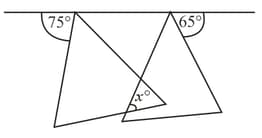
What is the measure of $x$?

In $△PQR$, $PQ=QR=RP=7\mathrm{cm}$, then find each angle of $△PQR$.

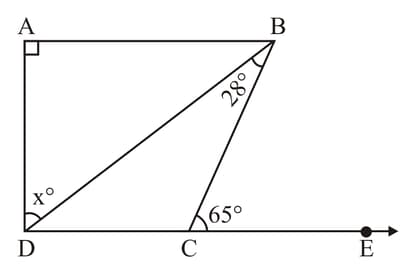
Given $AB\perp AD$ and $AB\parallel DC$. Find the value of the $x$ as shown in the below figure.

the values of $x \mathrm{and} y$ is $45° \mathrm{and} 120°$.

.

An external angle of a triangle is $115°$ and its interior opposite angles are equal. Then, each angle is _______$°$.

In a $∆ABC, \angle B=105°, \angle C=50°.$If $\angle A=k°$, then find $k$.

As a part of a campaign, a huge balloon with message of 'AWARENESS OF CANCER" was displayed from the terrace of a tall building. It was held by strings of length 8 m each, which inclined at an angle of $60°$ at the point, where it was tied as shown in the figure.

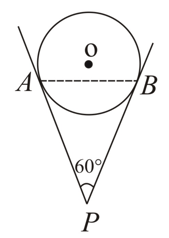
The perpendicular distance from the centre of the circle $A$ to the chord $AB$ is $3 \mathrm{m},$ if the radius of the circle is $k m$, then find the value of $k$.

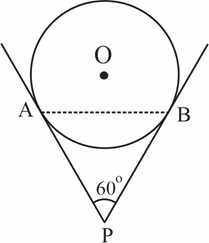
As a part of a campaign, a huge balloon with message of "AWARENESS OF CANCER" was displayed from the terrace of a tall building. It was held by strings of length $8 \mathrm{m}$ each, which are inclined at an angle of $60°$ at the point where it was tied as shown in the figure. If the length of $AB$ is $x \mathrm{m}$, then find the value of $x$.

$\mathrm{ABCD}$ is a cyclic quadrilateral and $\mathrm{PQ}$ is a tangent to the circle at $C$. If $\mathrm{BD}$ is a diameter, $\angle DCQ=40°$ and $\angle ABD=60°$ then find the measure of $\angle \mathrm{ADB}$ (write answer without degree symbol) is

In a $△ABC, \angle C=3\angle B=2(\angle A+\angle B)$. If the sum of $\angle A$ and $\angle B$ is $k°$, then $k$ is equal to

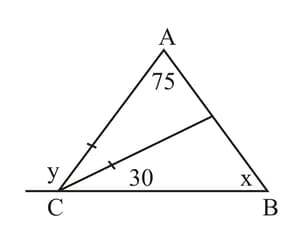Diagonals of a parallelogram $ABCD$ intersect at $O$. If $\angle BOC=90° \mathrm{and} \angle BDC=50°$, then $\angle OAB$ is