Area of a General Quadrilateral

The Diagonal $AC=15 cm$ of $ABCD$ and the lengths of the perpendiculars drawn from $B$ and $D$ to $AC$ are $3 cm$ and $5 cm$ respectively. Then find the area of the quadrilateral $ABCD$. 

The base of a parallelogram is $21 \mathrm{cm}$ and the corresponding height is $16 \mathrm{cm}$. A rhombus has the same area as the parallelogram. If one diagonal of the rhombus is $48 \mathrm{cm}$ find perimeter of the rhombus.

The base of a parallelogram is $21 \mathrm{cm}$ and the corresponding height is $16 \mathrm{cm}$. A rhombus has the same area as the parallelogram. If one diagonal of the rhombus is $48 \mathrm{cm}$ find other diagonal.

The diagonals of a rhombus are $32 \mathrm{cm}$  and $24 \mathrm{cm}$. Find its area in${\mathrm{cm}}^2$.(Do not write unit)

Shown below is rhombus $\mathrm{ABCD}.$

Its diagonals, $\mathrm{AC} = 24 \mathrm{cm}$ and $\mathrm{BD} = 10 \mathrm{cm},$

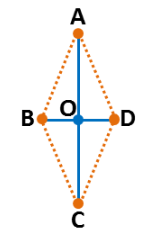
What is the length of its side $\mathrm{CD}$?

A goldsmith took the measurements around a Ruby stone and found it to be 12cm. What is this measurement?

Raju drew a Rhombus of side ‘a’ cm. His teacher told him to increase the side to 4 less than twice the current size. What will be the perimeter of the new rhombus?

The area of a rhombus is equal to the area of a triangle whose base and the corresponding altitude are $24.8 \mathrm{cm}$ and $16.5 \mathrm{cm}$ respectively. If one of the diagonals of the rhombus is $22 \mathrm{cm}$, let the length of the other diagonal be $k \mathrm{cm}$. Find the value of$k$ (up to one decimal place).

Find the area of a rhombus whose side is $6.5 \mathrm{cm}$ and altitude is $5 \mathrm{cm}.$ If one of its diagonal is $13 \mathrm{cm}$ long, let the length of other diagonal be $k \mathrm{cm}$. Find the value of $k$.

Each side of a rhombus is $13 \mathrm{cm}$ and one diagonal is $10 \mathrm{cm}$. Let the area of the rhombus is $k {\mathrm{cm}}^2$. Find the value of $k$.

Each side of a rhombus is $13 \mathrm{cm}$ and one diagonal is $10 \mathrm{cm}$. Let the length of its other diagonal be $k \mathrm{cm}$. Find value of $k$.

The diagonals of a rhombus are $12 \mathrm{cm}$ and $15 \mathrm{cm}$. The area of the rhombus is equal to

If the diagonal $d$ of a quadrilateral is doubled and the heights $h_1$ and $h_2$ falling on $d$ are halved, then the area of quadrilateral _____.

The area of a rhombus whose diagonals are $10 \mathrm{cm}$ and $20 \mathrm{cm}$ is equal to
 

An auditorium hall is in the shape of a rhombus such that the lengths of the two diagonals of the hall are $12 \mathrm{m}$ and $16 \mathrm{m}$. Find the cost of painting the floor at the rate of $₹ 6.50 \mathrm{per} \mathrm{sq}. \mathrm{m}$.

The length of a diagonal of a quadrilateral shaped field is $48 \mathrm{m}$ and the lengths of perpendiculars dropped on it from the remaining opposite vertices are $16 \mathrm{m}$ and $26 \mathrm{m}$. Find the area of the field.

If the lengths of two diagonals of a rhombus are $16 \mathrm{cm}$ and $30 \mathrm{cm}$, find the area and the length of the side of the rhombus.

To tile the floor of a room of dimensions $8 \mathrm{m} \times 4·8 \mathrm{m},$ rhombus-shaped tiles of diagonals $16 \mathrm{cm}$ and $12 \mathrm{cm}$ costing $₹24$ and square-shaped tiles of diagonal $16 \mathrm{cm}$ costing $₹28$ are available. Which type of tiles should be chosen to minimize the cost? How much can be saved by choosing the right type over the other?