Exploring Diagonals of Rectangles and Squares

$\mathrm{LMNP}$ is a rectangle. Which is not an expression for $\mathrm{PX}$?

Which step will come at second  place when we construct a square whose diagonal is $6 cm.$

The minimum number of dimensions needed to construct a rectangle is:

Prove that diagonals of rectangle are of equal length.

A quadrilateral ABCD has an area of $50 {\mathrm{cm}}^2$. The diagonals AC and BD bisect each other at O such that AO $=$OB and CO$=$OD. If AC $= 10 \mathrm{cm}$, then the quadrilateral ABCD represents ____.

The side of a square is $a \mathrm{cm}$. The ratio of its diagonal to its base is:

Can we construct a square $ABCD$ :One diagonal is $5 \mathrm{cm}$. 

Construct a square $\mathrm{PQRS}$ in which one diagonal $\mathrm{PR}=5 \mathrm{cm}$. 
Write answer Yes/ No.

The diagonals of a rectangle are of _____ length. $($equal$/$unequal$)$

Side of the square is $4 \mathrm{m}$. Then find the angle of made by diagonal with the side of square.

$\mathrm{ABCD}$ is a square of diagonal $18\sqrt{2}$. $\mathrm{M}$ is mid point of side $\mathrm{DC}$. Then find the length of $\mathrm{AM}$.

What is the longest rod that can be placed in a room which is $7$ metre long, $9$ metre broad and $\sqrt{29}$ metre high?

In a square, diagonals bisect each other at $90°$.

The diagonal of a square are_____.

The diagonal of a square is $12 cm$. What is the length (in $cm$) of its side?

What shape do you get by joining the end points of two lines each of length $7 \mathrm{cm}$ which bisect each other at right angles?

Draw two lines of $5 \mathrm{cm}$ which bisect each other. What shape is formed by joining the end points?

$\mathrm{ABCD}$ is a rectangle. $\mathrm{O}$ is the point of intersection of the diagonals." $\mathrm{O}$ is equidistant from $\mathrm{A}, \mathrm{B} \mathrm{and} \mathrm{C}$”. Is this true? Explain.

Identify the following quadrilateral with the given properties:
Diagonals are equal in length.

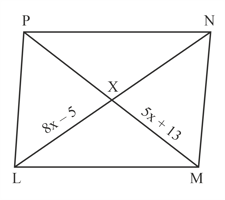
The diagonal of rectangle $\mathrm{ABCD}$ intersect each other at $\mathrm{O}.$ If $\angle \mathrm{BOC}={44}^{°}$, then the value of $\angle \mathrm{OAD}$ will be