Mid Point Theorem
Mid Point Theorem: Overview
This topic covers concepts such as properties of median, mid point theorem in a triangle, and mid point theorem in a quadrilateral.
Important Questions on Mid Point Theorem
Find the length of the median of the given triangle whole sides are given as follows, and , respectively, in which is the median formed on side .
If the length of each median of an equilateral triangle is then the perimeter of the triangle is
Show that the median of a triangle divides it into two triangles of equal areas
Prove that in an isosceles triangle the perpendicular drawn from the vertex angle to the base bisect the vertex angle and the base.
In figure, is the point of concurrence of medians of . Take point on ray such that and , then prove that is a parallelogram.
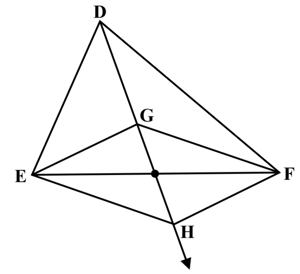
In is the mid-point of median such that produced meets at . If , then .
If and are respectively the midpoints of the sides and of in which and then determine the length of .
In the design below, assume there are 5 rectangles and 5 rhombuses. The 1st quadrilateral is a rectangle.
Which of the following numbers represents the innermost rectangle?
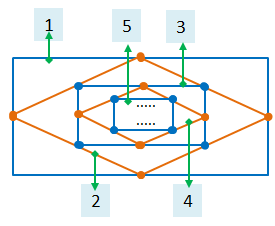
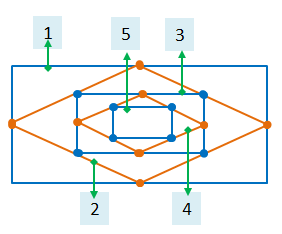
Assume there are 10 quadrilaterals in the design below.
Let $ {\text{A}}_{1}$ and $ {\text{A}}_{9}$ be the areas of the 1st and the 9th quadrilaterals.
Which of these formulae gives the correct relationship between $ {\text{A}}_{1}$ and $ {\text{A}}_{9}$?
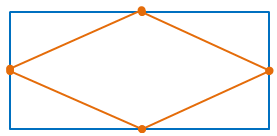
In the figure below, area of the rectangle is ‘A’. The midpoints of its sides are joined to get a rhombus.
What is the area of the rhombus inside the rectangle?
The cone below is cut by a plane parallel to its base to get two parts, where each part is half the height of the original cone.
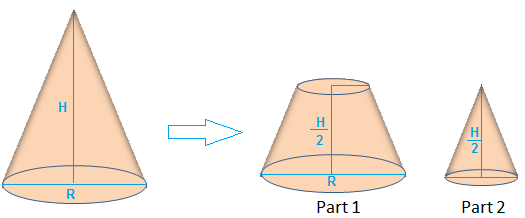
The ratio of the volumes of part1 to part2 is _____ : 1.
(The formula to find volume of cone, V=$ \frac{1}{3}$π$ {r}^{2}h$ where ‘R’ is the radius of its base and ‘H’ is its height.)
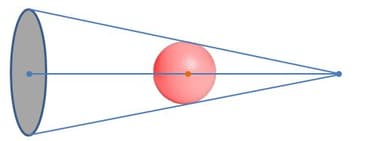
The figure below shows the shadow cast by a ball placed in the middle between a light source and the wall on which its shadow is projected.
If the radius of the ball is 5 cm, the area formed by the shadow of the ball is _____ sq cm.
(Note: Assume $ \pi $ = 3.14)
A carpenter is making a table top which is the shape of a right angle triangle by picking one of the pairs of plywood pieces and joining them. (Along the red line)
Which of the following pairs should the carpenter choose to form the table top?
(Note: Figures not to scale. Make your choice based on the measurements only.)
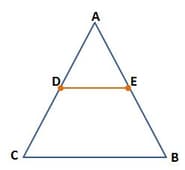
In △ABC, D and E are the midpoints of its sides AB and AC.
If the area of △ABC = 100 sq units, then the area of the quadrilateral BCDE = _____ sq units.
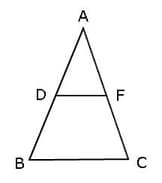
The line DF through the midpoint of sides AB and AC of ∆ABC is 15 cm.
Length of side BC = _____ cm
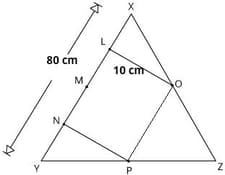
Ravi made a few markings on a triangular board, as shown in the figure below. He marked in such a way that XL = LM= MN= NY. Total length XY = 80 cm and OL = 10 cm.
If he cuts a quadrilateral LNPO and sticks picture tape along its edges, then the total length of the picture tape required = _____ cm
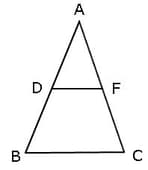
In the given triangle D and F are mid points of AB and AC.
AB = 12 cm, BC = 15 cm and CA = 17 cm.
The perimeter of the trapezium BCFD = _____ cm.
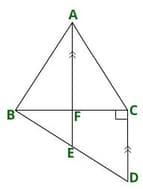
An equilateral triangle board is attached to a right angled triangle as shown below. E and F are points on BD and BC.
If the measure of DE = 10 cm, then the measure of BD = _____ cm.
In the following figure, BC = 24 cm.
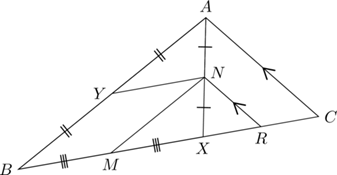
Length of MR = _____ cm.
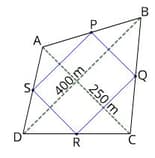
Hari had a quadrilateral patch of land and he wanted to make it a proper playground. He made a plan for the land ABCD and marked P, Q, R, S as the mid points of AB, BC, CD and DA respectively. He then decided to remove the outer triangular regions.
The perimeter of the plot PQRS = _____ m