Square and its Properties

The diagonals of a square with area $9 {\mathrm{m}}^2$ divide the square into four non-overlapping triangles. What is the sum of the perimeter of the four triangles.

$△BEF$ and $△FED$ are two isosceles triangles in the square $ABCD$. What is the measure of $\angle FBE$?

Number of sides square has.

Consider the following statements :

$\left(\mathrm{i}\right)$ The diagonals of a parallelogram are equal.

$\left(\mathrm{ii}\right)$ The diagonals of a square are perpendicular to each other.

$\left(\mathrm{iii}\right)$ If the diagonals of a quadrilateral intersect at right angles, it is not necessarily a rhombus.

$\left(\mathrm{iv}\right)$ Every quadrilateral is either a parallelogram or a kite or a trapezium.

Which of the above statements is/are correct?

A parallelogram will become a square when

A quadrilateral can be a square if

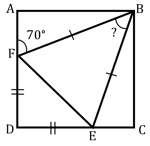
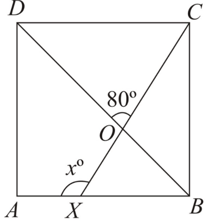
In the adjoining figure, $PQRS$ is a square. A line segment $RX$ cuts $PQ$ at $\mathrm{X}$ and the diagonal $QS$ at $\mathrm{O}$ such that $\angle ROS=60°$ and $\angle \mathrm{OX}Q=x°$. Find the value of $x$. (Give the answer in value without degree symbol).

Write the conditions for the quadrilateral $ABCD$ to be a square.

The four angles of a quadrilateral are congruent and the four sides of a quadrilateral are also congruent. Then, the quadrilateral is a

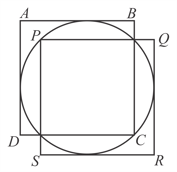
The diagram shows two identical squares, $ABCD$ and $PQRS$, overlapping each other in such a way that their edges are parallel, and a circle of radius $(2-\sqrt{2}) \mathrm{cm}$ covered within these squares. Find the length of the side of square $ABCD.$

A square and a parallelogram have the same area. If the side of the square is $48\mathrm{m}$ and the height of the parallelogram is $18\mathrm{m}$. Find the length of the base of the parallelogram.

How are square and parallelogram alike?

Is a square a parallelogram?

A square can be a parallelogram.

What is the relation between square and a parallelogram?

Diagonals of a parallelogram are of equal length and intersect at right angle, then the parallelogram is

In the adjoining figure, $\mathrm{ABCD}$ is a square. A line segment $\mathrm{CX}$ cuts $\mathrm{AB}$ at $\mathrm{X}$ and the diagonal $\mathrm{BD}$ at $\mathrm{O}$ such that $\angle \mathrm{COD}=80°$ and $\angle \mathrm{OXA}=x°$. Find the value of $x$. (Give the answer in value without degree symbol).

Let $ABCD$ be a square. An arc of a circle with $A$ as centre and $AB$ as radius is drawn inside the square joining the points $B$ and $D$. Points $P$ on $AB, S$ on $AD, Q$ and $R$ on arc $BD$ are taken such that $PQRS$ is a square. Further suppose that $PQ$ and $RS$ are parallel to $AC$. Then, $\frac{\text{ area }PQRS}{\text{ area }ABCD}$ is

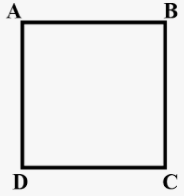
Here is a square is drawn for you. Is $\angle ADO=\angle CDO$?

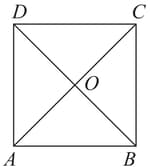
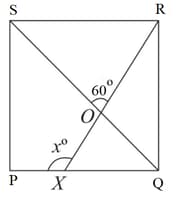
In a square $ABCD$, $AB=\left(2x+3\right) \mathrm{cm}$ and $BC=\left(3x-5\right) \mathrm{cm}$. Then the value of $x$ is