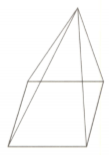
Part of Solid Shapes and Euler's Formula
Part of Solid Shapes and Euler's Formula: Overview
Via this topic, we will learn the definitions of face, edge and vertex of a solid figure. These are the elements of a solid figure. It also explains Euler's formula and its application for the solid shapes.
Important Questions on Part of Solid Shapes and Euler's Formula
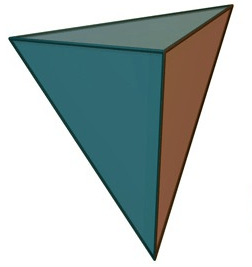
For tetrahedron shape prove the Euler’s Formula.
Use Euler's Theorem to calculate how many vertices a polyhedron has if it has faces and edges.
Given figure has how many curved edges

A circle have straight edges.
A cone has _____ curved edges:
Which shape has curved edge?
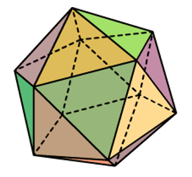
Icosahedron has 20 faces and 30 edges. The number of vertices for the icosahedron will be _____
What will be the number of faces, edges and vertices of a pyramid whose base is a polygon of N sides ?
Can a simple solid have 6 edges and 7 vertices? Verify using Euler’s formula.
What will the number of faces be for a structure of a molecule which has 60 carbon atoms that are joined together by 90 bonds?

The following image satisfies Euler’s formula.
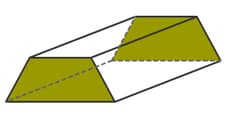
If this is cut by a horizontal plane, then will the lower portion of the cut solid (frustum) satisfy the Euler’s formula?
What is the name of the polyhedron with 10 faces and 16 vertices?
The solid shown below does not satisfy the Euler’s formula as that solid is a concave polyhedron. How can you cut the solid in such a way that both the cut pieces satisfy the Euler’s formula.

Is there any simple regular polyhedron that has exactly ten faces and seventeen vertices?
Euler’s formula can be applied to all the polyhedrons. Is this statement correct?
Identify the solid that does not satisfy the Euler’s formula.
The value of the Euler’s formula, F+V-E for a cube is _____.
Can a polyhedron have faces, edges and vertices?
Verify Euler's formula for the following solid (show calculations).
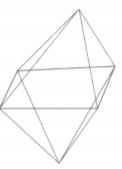
Verify Euler's formula for the following solid (show calculations).