Length of a Line Segment
Length of a Line Segment: Overview
This topic covers concepts, such as, Distance of a Point from the Origin, Finding Distance with Pythagoras Theorem & Midpoint of a Line Segment etc.
Important Questions on Length of a Line Segment
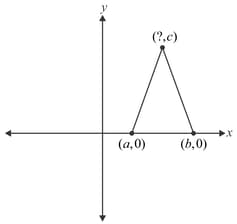
The coordinates of the vertices of an isosceles triangle are shown. The -coordinate of one of the vertices is missing. Which expression represents the missing -coordinate?
Find the distance between the point and the origin.
A variable line in a plane passes through a fixed point and meets the coordinate axes at points and . Then the locus of the mid-point of is
What is the distance of point from the origin?
If a line has the equation and it passes through the point Then find the slope of this line
Amul conducted a survey he cheek locking of ice cream flowered among vanilla, chocolate, strawberry for Per so people like all Ice cream flavours, same no of people like, chocolate &strawberry. The people who like vanilla & chocolate is & People who like strawberry & vanilla is people like vanilla flavour. If people do not like any flavour & people who like only chocolate is equal to who like only strawberry .
What is the no of people who like only chocolate flavour.
The points forms a
The point is at a distance of units from the line What is the value of ?
The three vertices of a parallelogram taken in order are and respectively. Find the coordinates of the fourth vertex.
If the middle points of the sides of a triangle are and , find the centroid of the triangle.
The three vertices of a parallelogram are respectively, find the co-ordinates of vertex .
What is the radius of a circle, if the centre of the circle is at and the point lies on the circle.
The distance of the point from the origin is-
If the midpoints of the sides of a triangle are and then find the coordinates of its vertices.
Let and let and be the vertices of a parallelogram . If and the points and lie on the line , then is equal to
Cotyledons are also called-
If the coordinates of the vertices of the triangle be and respectively, then the equation of the median through is
Vertices of a quadrilateral are and . Then quadrilateral is
If mid point of and is then value of is
The coordinates of midpoints of the sides of a triangle are . Then sum of lengths of sides of the triangle is
