Altitude of a Triangle
Altitude of a Triangle: Overview
This topic covers concepts, such as Altitude of Triangles, Altitudes and Medians in Equilateral Triangles, and Basic Properties of Altitudes of Triangles.
Important Questions on Altitude of a Triangle
Name the orthocentre of .
Identify the type of segment required in the below triangle:
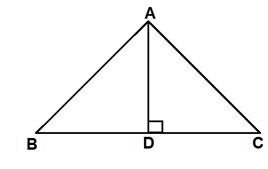
Median and altitude of an equilateral triangle coincide.
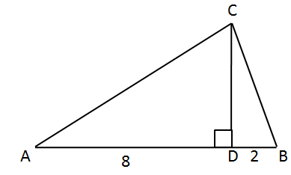
is a right angled triangle. If then find .
If the altitude to side of triangle with side is then find .
If the altitude of a triangle is , its area is and its base is then find .
If the altitude of an equilateral triangle when its equal sides are given as is then find .
Every triangle has altitudes, one from each vertex.
The orthocenter is located inside the triangle in _____ triangle. (Acute/Right)
Given: is the altitude, . If then find .
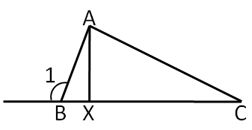
Given: is the altitude, . If is then find
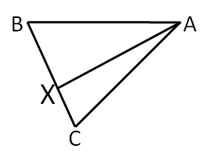
Where does the orthocentre lie in the case of a right angled triangle?
Where does the orthocentre lie in the case of an obtuse-angled triangle?
Where does the orthocentre lie in the case of an acute-angled triangle?
The altitudes of a triangle intersect at _____.
The area of a circle inscribed in an equilateral triangle is . The length of altitude of triangle is:
Draw all three altitudes for the following triangles and explain how they are different:
is the centroid of the equilateral . If , then length of the is :
